Exam 5: Matrix Algebra and Applications
Exam 1: Functions and Applications159 Questions
Exam 2: Nonlinear Functions and Models92 Questions
Exam 3: The Mathematics of Finance137 Questions
Exam 4: Systems of Linear Equations and Matrices111 Questions
Exam 5: Matrix Algebra and Applications174 Questions
Exam 6: Linear Programming161 Questions
Exam 7: Sets and Counting154 Questions
Exam 8: Probability257 Questions
Exam 9: Random Variables and Statistics178 Questions
Exam 10: Introduction to the Derivative139 Questions
Exam 11: Techniques of Differentiation104 Questions
Exam 12: Applications of the Derivative88 Questions
Exam 13: The Integral66 Questions
Exam 14: Further Integration Techniques and Applications of the Integral118 Questions
Exam 15: Functions of Several Variables137 Questions
Exam 16: Trigonometric Models67 Questions
Select questions type
Production of 1 unit of cologne requires 0.9 units of perfume and 0.4 units of cologne. Into 1 unit of perfume goes 0.2 unit of perfume and 0.5 units of cologne. With sector 1 as cologne and sector 2 as perfume, set up the technology matrix A.
(Multiple Choice)
4.8/5  (21)
(21)
You are deciding whether to invade Japan, Sweden or Canada, and your opponent is simultaneously deciding which of these three countries to defend. If you invade a country that your opponent is defending, you will be defeated (payoff: -2), but if you invade a country your opponent is not defending, you will be successful (payoff: +2). Set up the payoff matrix with you as the row player and your opponent as the column player.
(Essay)
4.7/5  (34)
(34)
Determine if the given pair of matrices is an inverse pair. Explain your work.
,
(Essay)
4.8/5  (31)
(31)
Compute the product of the two matrices (if possible).
If the product is not defined please enter undefined.
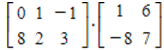
(Short Answer)
4.7/5  (26)
(26)
Given the technology matrix A, and an external demand vector D, find the production vector X.
,
(Multiple Choice)
4.9/5  (37)
(37)
The chart shows the number of personal bankruptcy filings in three City regions during various months of 2001 - 2002. Jan 01 Jul 01 Jan 02 North 130 130 130 West 310 310 250 East 250 250 180
Write a matrix product whose computation gives the total number by which bankruptcy filings in January, 2001, exceeded filings in January, 2002.
Enter your answer in the form , where A is the matrix, B is the matrix, C is the matrix, and D is the matrix.
(Essay)
4.8/5  (32)
(32)
Use row reduction to find the inverse of the given matrix, if it exists, and check your answer by multiplication.
(Essay)
4.9/5  (31)
(31)
In January, the Left Coast Bookstore chain sold 900 hardcover books, 1,200 softcover books, and 1,600 plastic books in San Francisco; it sold 600 hardcover, 500 softcover, and 700 plastic books in Los Angeles. Hardcover books sell for $34 each, softcover books sell for $8 each, and plastic books sell for $14 each. Hard Soft Plastic San Francisco 900 1,200 1,600 Los Angeles 600 500 700
Suppose that each hardcover book costs the stores $10, each softcover book costs $5, and each plastic book costs $10.
Use matrix operations to compute the the total profit at each store in January.
Please enter your answer as a column matrix in the following form:
(Essay)
4.7/5  (35)
(35)
For the given row strategy R, find the optimal pure strategy (or strategies) the other player should use. Express the answer as a row or column matrix. Also determine the resulting expected value of the game. ,
(Multiple Choice)
4.8/5  (33)
(33)
Four sectors of some economy are (1) Sector 1, (2) Sector 2, (3) Sector 3, and (4) Sector 4. The input-output table involving these four sectors was as follows (all figures are in millions of dollars): To 1 2 3 4 From 174.3 30.7 120.4 14.1 0 190.2 55.9 12.4 2 40.9 1,418.1 1,242.1 0.1 7.1 40.7 326.2 Total Output 3,278 2,188.5 6,541.1 4,065.7
How much additional production by the Sector 1 is necessary to accommodate a $1,000 increase in the demand for the products of Sector 4 Round your answer to two decimal places.
$ __________ million
(Short Answer)
4.7/5  (36)
(36)
For the given row strategy R, find the optimal pure strategy (or strategies) the other player should use. Express the answer as a row or column matrix. ,
(Multiple Choice)
4.9/5  (41)
(41)
Given the technology matrix A, and an external demand vector B, find the production vector X.
,
(Essay)
4.9/5  (39)
(39)
Translate the matrix equations into a system of linear equations.
(Multiple Choice)
4.8/5  (40)
(40)
Use matrix inversion to solve the given system of linear equations. 2x-3y-2z =5 -z =1 x-2y+2z =-9
(Multiple Choice)
5.0/5  (42)
(42)
Use matrix inversion to solve the system of linear equations. x+2y+z =8 x+y+z =7 3x+y+z =25
(Multiple Choice)
4.9/5  (40)
(40)
When you bet on a racehorse with odds of m-n, you stand to win m dollars for every bet of n dollars if your horse wins; for instance, if the horse you bet is running at 5-2 and wins, you will win $5 for every $2 you bet. (Thus a $2 bet will return $7.). Here are some actual odds from a 1992 race at Belmont Park, NY. The favorite at 4-1 was Pleasant Tap. The second choice was Thunder Rumble at 7-2, while the third choice was Strike the Gold at 7-2. Assume you are making a $20 bet on one of these horses. The payoffs are your winnings. (If your horse does not win, you lose your entire bet. Of course, it is possible for none of your horses to win.) Suppose that just before the race, there has been frantic betting on Thunder Rumble, with the result that the odds have dropped to 1-5. The odds on the other two horses remain unchanged. Set up the payoff matrix with your bet as the row player and winner as the column player.
Let the first column correspond to Pleasant Tap, the second one to Thunder Rumble, the third one to Strike the Gold and the first row correspond to Pleasant Tap, the second one to Thunder Rumble, the third one to Strike the Gold .
(Essay)
4.8/5  (34)
(34)
Showing 21 - 40 of 174
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)