Exam 5: Matrix Algebra and Applications
Exam 1: Functions and Applications159 Questions
Exam 2: Nonlinear Functions and Models92 Questions
Exam 3: The Mathematics of Finance137 Questions
Exam 4: Systems of Linear Equations and Matrices111 Questions
Exam 5: Matrix Algebra and Applications174 Questions
Exam 6: Linear Programming161 Questions
Exam 7: Sets and Counting154 Questions
Exam 8: Probability257 Questions
Exam 9: Random Variables and Statistics178 Questions
Exam 10: Introduction to the Derivative139 Questions
Exam 11: Techniques of Differentiation104 Questions
Exam 12: Applications of the Derivative88 Questions
Exam 13: The Integral66 Questions
Exam 14: Further Integration Techniques and Applications of the Integral118 Questions
Exam 15: Functions of Several Variables137 Questions
Exam 16: Trigonometric Models67 Questions
Select questions type
Four sectors of some economy are (1) Sector 1, (2) Sector 2, (3) Sector 3, and (4) Sector 4. The input-output table involving these four sectors was as follows (all figures are in millions of dollars)
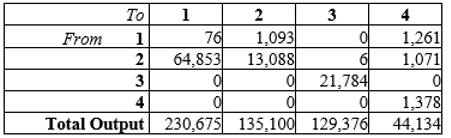
(Essay)
4.8/5  (31)
(31)
Two sectors of some economy are Sector 1 and Sector 2. The input-output table involving these two sectors results in the following value for
How many additional dollars worth of production of Sector 2 must be produced to meet a $1 increase in the demand for products of Sector 2
(Multiple Choice)
4.9/5  (29)
(29)
Let be the technology matrix, be the production vector, and be the external demand vector.
There would be 0.4 units of sector 2 needed to produce one unit of sector 2.
(True/False)
4.9/5  (35)
(35)
Let and assume that the external demand for the products in Sector 1 increases by 1 unit. By how many units should each sector increase production
?
Express the answer as a column matrix.
(Essay)
4.9/5  (32)
(32)
Four sectors of some economy are (1) Sector 1, (2) Sector 2, (3) Sector 3, and (4) Sector 4. The input-output table involving these four sectors was as follows (all figures are in millions of dollars) To 1 2 3 4 From 681.8 3,106.9 1,033.5 12.8 7.2 15 103.4 48.3 4.5 855.9 112.3 348.7 22.5 82.1 693.7 Total Output 9,375.7 663.2 6,510.3 4,865.8
How much additional production by the Sector 3 is necessary to accommodate a $100 increase in the demand for the products of Sector 1 Round your answers to two decimal places.
$ __________
(Short Answer)
4.8/5  (41)
(41)
Reduce the payoff matrix by dominance.
B p q r a A b 3 0 12 14 -2 -5
(Essay)
4.8/5  (37)
(37)
Let and assume that the external demand for the products in each of the sectors increases by 1 unit. By how many units should each sector increase production
(Multiple Choice)
4.8/5  (31)
(31)
Use row reduction to find the inverse of the given matrix, if it exists, and check your answer by multiplication.
(Short Answer)
4.7/5  (33)
(33)
Your fast-food outlet, Burger Queen, has obtained a license to open branches in three closely situated South African cities: Brakpan, Nigel, and Springs. Your market surveys show that Brakpan and Nigel each provide a potential market of 2,500 burgers a day, while Springs provides a potential market of 1,000 burgers per day. Your company can only finance an outlet in one of those cities at the present time. Your main competitor, Burger Princess, has also obtained licenses for these cities, and is similarly planning to open only one outlet. If you both happen to locate at the same city, you will share the total business from all three cities equally, but if you locate in different cities, you will each get all the business in the cities in which you have located, plus half the business in the third city. The payoff is the number of burgers you will sell per day minus the number of burgers your competitor will sell per day. Set up the payoff matrix with you as the row player and your opponent as the column player.
Let the first column correspond to Brakpan, the second one to Nigel, the third one to Springs and the first row correspond to the Brakpan, the second one to the Nigel, the third one to Springs.
(Essay)
4.9/5  (31)
(31)
Find the dimensions of the matrix
And identify the value of the element .
(Multiple Choice)
4.7/5  (42)
(42)
Determine whether or not the pair of matrices is an inverse pair. ,
(Multiple Choice)
4.8/5  (48)
(48)
Your Abercrom B men's fashion outlet has a 60% chance of launching an expensive new line of used auto-mechanic dungarees (complete with grease stains) and a 40% chance of staying instead with its traditional torn military-style dungarees. Your rival across from you in the mall, Abercrom A, appears to be deciding between a line of torn gym shirts and a more daring line of "empty shirts" (that is, empty shirt boxes). Your corporate spies reveal that there is a 50% chance that Abercrom A will opt for the empty shirt option. The payoff matrix gives the number of customers your outlet can expect to gain from Abercrom A in each situation.
? Abercrom A Torn Empty Shirts Shirts Abercrom B Mechanics Military 10 -40 -30 50 ?
How many customers can you expect to lose Round the answer to the nearest whole.
?
__________ customers
(Short Answer)
4.9/5  (37)
(37)
Use the row reduction method to find the inverse of the given matrix, if it exists.
(Essay)
4.8/5  (39)
(39)
Use matrix inversion to solve the system of linear equations. 2x+3y-2z =-11 x+y+z =5 x+2y-z =-4
(Multiple Choice)
4.8/5  (29)
(29)
Use matrix inversion to solve the given system of linear equations.
2x+11y-2z=2 x+y+z=0 x+6y-z=2
(Short Answer)
4.9/5  (28)
(28)
Use matrix inversion to solve the given system of linear equations.
5x+3y=1 3x+2y=6
(Short Answer)
4.7/5  (38)
(38)
Showing 101 - 120 of 174
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)