Exam 10: Introduction to the Derivative
Exam 1: Functions and Applications159 Questions
Exam 2: Nonlinear Functions and Models92 Questions
Exam 3: The Mathematics of Finance137 Questions
Exam 4: Systems of Linear Equations and Matrices111 Questions
Exam 5: Matrix Algebra and Applications174 Questions
Exam 6: Linear Programming161 Questions
Exam 7: Sets and Counting154 Questions
Exam 8: Probability257 Questions
Exam 9: Random Variables and Statistics178 Questions
Exam 10: Introduction to the Derivative139 Questions
Exam 11: Techniques of Differentiation104 Questions
Exam 12: Applications of the Derivative88 Questions
Exam 13: The Integral66 Questions
Exam 14: Further Integration Techniques and Applications of the Integral118 Questions
Exam 15: Functions of Several Variables137 Questions
Exam 16: Trigonometric Models67 Questions
Select questions type
At which labeled point is the slope of the tangent line greatest ? 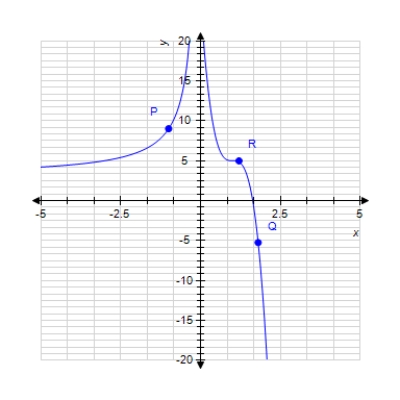 ?
?
(Multiple Choice)
4.8/5  (39)
(39)
Estimate the derivative of the function at the point .
Please round your answer to the nearest hundredth.
(Short Answer)
4.9/5  (36)
(36)
Calculate the average rate of change of the given function over the interval . t (month) 2 4 6 (t)( ( millions) 13.2 13.8 12.6
(Multiple Choice)
4.8/5  (37)
(37)
The function given below gives the cost to manufacture items. Estimate (using ) the instantaneous rate of change of the cost at the production level .
Select your answer rounded to the nearest tenth.
(Multiple Choice)
4.9/5  (33)
(33)
Calculate the average rate of change of the given function over the interval .
(Multiple Choice)
4.7/5  (31)
(31)
Give an example of a function that is not continuous at but is not discontinuous there either.
(Essay)
4.7/5  (26)
(26)
Calculate the average rate of change of the given function over the interval .
(Multiple Choice)
4.8/5  (39)
(39)
The function given below gives the cost to manufacture x items. Estimate (using ) the instantaneous rate of change of the total cost at the production level .
Select your answer rounded to the nearest tenth.
(Multiple Choice)
4.8/5  (36)
(36)
The graph of a function f is given. Determine whether f is continuous on its domain.
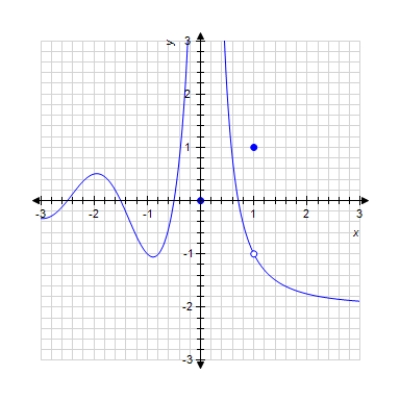
(Multiple Choice)
4.9/5  (31)
(31)
Showing 121 - 139 of 139
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)