Question 1

Administering the same test to a group of 15 students and a second group of 15 students to see which group scores higher is an example of:

Accepted Answer

A)  a one sample test of means. 
B)  a two sample test of means. 
C)  a paired t-test. 
D)  a test of proportions. 
E)  None of these statements is correct. 
A)  a one sample test of means. 
B)  a two sample test of means. 
C)  a paired t-test. 
D)  a test of proportions. 
E)  None of these statements is correct.

Question 2

i. If samples taken from two populations are not independent, then a test of paired differences is applied.
Ii) The paired difference test has (n - 1) degrees of freedom.
Iii) The paired t test is especially appropriate when the sample sizes of two groups are the same.

Accepted Answer

A)  (i), (ii) and (iii) are all correct statements 
B)  (i) and (ii) are correct statements, but not (iii). 
C)  (i) and (iii) are correct statements but not (ii). 
D)  (ii) and (iii) are correct statements but not (i). 
E)  (ii) is a correct statement, but not (i) and (iii). 
A)  (i), (ii) and (iii) are all correct statements 
B)  (i) and (ii) are correct statements, but not (iii). 
C)  (i) and (iii) are correct statements but not (ii). 
D)  (ii) and (iii) are correct statements but not (i). 
E)  (ii) is a correct statement, but not (i) and (iii).

Question 3

The net weights of a sample of bottles filled by a machine manufactured by Edne, and the net weights of a sample filled by a similar machine manufactured by Orno, Inc., are (in grams):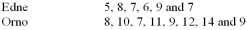   
Testing the claim at the 0.05 level the mean weight of the bottles filled by the Orno machine is greater than the mean weight of the bottles filled by the Edne machine, what is the critical value?

Accepted Answer

A)  -1.96 
B)  -2.837 
C)  -6.271 
D)  +3.674 
E)  None of these statements is correct 
A)  -1.96 
B)  -2.837 
C)  -6.271 
D)  +3.674 
E)  None of these statements is correct

Question 4

A national manufacturer of ball bearings is experimenting with two different processes for producing precision ball bearings. It is important that the diameters be as close as possible to an industry standard. The output from each process is sampled and the average error from the industry standard is calculated. The results are presented below.   The researcher is interested in determining whether there is evidence that the two processes yield different average errors.
What is the computed value of t?

Accepted Answer

A)  +2.797 
B)  -2.797 
C)  -13.70 
D)  +13.70 
E)  None of these statements are correct. 
A)  +2.797 
B)  -2.797 
C)  -13.70 
D)  +13.70 
E)  None of these statements are correct.

Question 5

A recent study compared the time spent together by single and dual-earner couples. According to the records kept during the study, the mean amount of time spent together watching TV among single- earner couples was 60 minutes per day, with a standard deviation of 15.5 minutes. For the dual-earner couples, the mean time was 48.4 and the standard deviation was 18.1. At a 0.01 significance level, can we conclude that the single-earner couples on average spend more time watching TV together? There were 12 single-earner and 12 dual-earner couples studied. State the decision rule, the value of the test statistic, and your decision.

Accepted Answer

A)  Reject if t > 2.485, t = 2.77, single-earner couples spend more time watching TV together. 
B)  Reject if t > 2.508, t = 1.96, insufficient evidence to say that single-earner couples spend more time watching TV together. 
C)  Reject if t > 2.797, t = 2.57, single-earner couples spend more time watching TV together. 
D)  Reject if t > 2.508, t = 1.69, insufficient evidence to say that single-earner couples spend more time watching TV together. 
E)  Reject if t > 2.508, t = 0.96, insufficient evidence to say that single-earner couples spend more time watching TV together. 
A)  Reject if t > 2.485, t = 2.77, single-earner couples spend more time watching TV together. 
B)  Reject if t > 2.508, t = 1.96, insufficient evidence to say that single-earner couples spend more time watching TV together. 
C)  Reject if t > 2.797, t = 2.57, single-earner couples spend more time watching TV together. 
D)  Reject if t > 2.508, t = 1.69, insufficient evidence to say that single-earner couples spend more time watching TV together. 
E)  Reject if t > 2.508, t = 0.96, insufficient evidence to say that single-earner couples spend more time watching TV together.

Question 6

The results of a mathematics placement exam at Mercy College for two campuses is as follows: 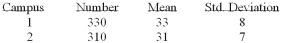  We want to test the hypothesis that the mean score on Campus 1 is higher than on Campus 2.   Using the printout above, what decision(s) can be made?

Accepted Answer

A)  Looking at the P-value we conclude that there is no significant difference in the results from each campus 
B)  At a 5% level of significance we conclude that there is no significant difference in the results from each campus 
C)  At a 1% level of significance we conclude that campus 1 results are higher than campus 2 results 
D)  A & B are true 
E)  B & C are true 
A)  Looking at the P-value we conclude that there is no significant difference in the results from each campus 
B)  At a 5% level of significance we conclude that there is no significant difference in the results from each campus 
C)  At a 1% level of significance we conclude that campus 1 results are higher than campus 2 results 
D)  A & B are true 
E)  B & C are true

Question 7

Married women are more often than not working outside the home on at least a part-time basis, as do most mannered men. Does a husband's employment status affect his wife's well being? In an attempt to answer this question, 20 married female professionals were surveyed as to their job satisfaction.
In this sample, 15 husbands were employed, and 5 were unemployed. The Learning Objective of the study was to compare the mean job satisfaction levels of the married women with working husbands, with the mean job satisfaction levels of the married women with husbands that stayed at home.
If the p-value obtained from the computer printout is 0.025, does this give sufficient evidence to conclude that the mean level of job satisfaction for women with working husbands is more than that of those whose husbands don't work?

Accepted Answer

A)  Yes, at alpha = 0.05 
B)  Yes, at alpha = 0.01 
C)  No, at alpha = 0.10 
D)  No, at alpha = 0.04 
E)  Insufficient information to make a decision 
A)  Yes, at alpha = 0.05 
B)  Yes, at alpha = 0.01 
C)  No, at alpha = 0.10 
D)  No, at alpha = 0.04 
E)  Insufficient information to make a decision

Question 8

A national manufacturer of ball bearings is experimenting with two different processes for producing precision ball bearings. It is important that the diameters be as close as possible to an industry standard. The output from each process is sampled and the average error from the industry standard is calculated. The results are presented below.   The researcher is interested in determining whether there is evidence that the two processes yield different average errors. Assume calculated t to be +2.70; at the 0.01 level of significance what would be the decision?

Accepted Answer

A)  Reject the null hypothesis and conclude the means are different. 
B)  Reject the null hypothesis and conclude the means are the same. 
C)  Fail to reject the null hypothesis and conclude the means are the same. 
D)  Fail to reject the null hypothesis and conclude the means are different. 
E)  None of these statements are correct. 
A)  Reject the null hypothesis and conclude the means are different. 
B)  Reject the null hypothesis and conclude the means are the same. 
C)  Fail to reject the null hypothesis and conclude the means are the same. 
D)  Fail to reject the null hypothesis and conclude the means are different. 
E)  None of these statements are correct.

Question 9

A recent study compared the time spent together by single and dual- earner couples. According to the records kept during the study, the mean amount of time spent together watching TV among single- earner couples was 55 minutes per day, with a standard deviation of 15.5 minutes. For the dual-earner couples, the mean time was 48.4 and the standard deviation was 18.1. At a 0.01 significance level, can we conclude that the single-earner couples on average spend more time watching TV together? There were 12 single-earner and 12 dual-earner couples studied. State the decision rule, the value of the test statistic, and your decision.

Accepted Answer

A)  Reject if t > 2.485, t = 2.57, insufficient evidence to say that single-earner couples spend more time watching TV together. 
B)  Reject if t > 2.508, t = 0.96, insufficient evidence to say that single-earner couples spend more time watching TV together. 
C)  Reject if t > 2.473, t = 2.57, single-earner couples spend more time watching TV together. 
D)  Reject if t > 2.508, t = 0.96, single-earner couples spend more time watching TV together. 
E)  Reject if t > 2.485, t = 2.01, single-earner couples spend more time watching TV together. 
A)  Reject if t > 2.485, t = 2.57, insufficient evidence to say that single-earner couples spend more time watching TV together. 
B)  Reject if t > 2.508, t = 0.96, insufficient evidence to say that single-earner couples spend more time watching TV together. 
C)  Reject if t > 2.473, t = 2.57, single-earner couples spend more time watching TV together. 
D)  Reject if t > 2.508, t = 0.96, single-earner couples spend more time watching TV together. 
E)  Reject if t > 2.485, t = 2.01, single-earner couples spend more time watching TV together.

Question 10

To compare the effect of weather on sales of soft drinks, a soda manufacturer sampled two regions of the country with the following results. Is there a difference in sales between the 2 regions? 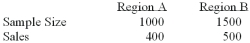  i. The null hypothesis is pa - pb > 0
Ii) The alternate hypothesis is pa - pb ≠ 0
Iii) The pooled estimate of the population proportion is 0.36.

Accepted Answer

A)  (i), (ii) and (iii) are all correct statements 
B)  (i) and (ii) are correct statements, but not (iii). 
C)  (i) and (iii) are correct statements but not (ii). 
D)  (ii) and (iii) are correct statements but not (i). 
E)  (ii) is a correct statement, but not (i) and (iii). 
A)  (i), (ii) and (iii) are all correct statements 
B)  (i) and (ii) are correct statements, but not (iii). 
C)  (i) and (iii) are correct statements but not (ii). 
D)  (ii) and (iii) are correct statements but not (i). 
E)  (ii) is a correct statement, but not (i) and (iii).

Question 11

A local retail business wishes to determine if there is a difference in preferred indoor temperature between men and women. A random sample of data is collected, with the following results (note:
There are slight differences between Excel and MegaStat output in this test): 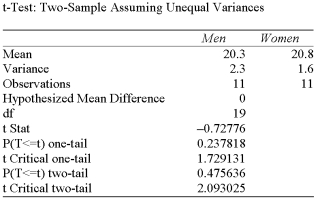  If you use the 5% level of significance, what is the critical t value?

Accepted Answer

A)  2.093 
B)  2.086 
C)  1.729 
D)  1.725 
E)  None of these statements are correct. 
A)  2.093 
B)  2.086 
C)  1.729 
D)  1.725 
E)  None of these statements are correct.

Question 12

To compare the effect of weather on sales of soft drinks, a soda manufacturer sampled two regions of the country with the following results. Is there a difference in sales between the 2 regions? 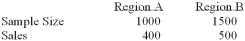  i. The null hypothesis is pa - pb = 0
Ii) The alternate hypothesis is pa - pb ≠ 0
Iii) Using the 1% level of significance, the critical value is ±2.58.

Accepted Answer

A)  (i), (ii) and (iii) are all correct statements 
B)  (i) and (ii) are correct statements, but not (iii). 
C)  (i) and (iii) are correct statements but not (ii). 
D)  (ii) and (iii) are correct statements but not (i). 
E)  (ii) is a correct statement, but not (i) and (iii). 
A)  (i), (ii) and (iii) are all correct statements 
B)  (i) and (ii) are correct statements, but not (iii). 
C)  (i) and (iii) are correct statements but not (ii). 
D)  (ii) and (iii) are correct statements but not (i). 
E)  (ii) is a correct statement, but not (i) and (iii).

Question 13

A recent study compared the time spent together by single and dual-earner couples. According to the records kept during the study, the mean amount of time spent together watching TV among single- earner couples was 64 minutes per day, with a standard deviation of 15.5 minutes. For the dual-earner couples, the mean time was 48.4 and the standard deviation was 18.1. At a 0.01 significance level, can we conclude that the single-earner couples on average spend more time watching TV together? There were 20 single-earner and 12 dual-earner couples studied. State the decision rule, the value of the test statistic, and your decision.

Accepted Answer

A)  Reject if t > 2.457, t = 2.59, single-earner couples spend more time watching TV together. 
B)  Reject if t > 2.508, t = 0.96, insufficient evidence to say that single-earner couples spend more time watching TV together. 
C)  Reject if t > 2.797, t = 2.57, single-earner couples spend more time watching TV together. 
D)  Reject if t > 2.042, t = 1.96, insufficient evidence to say that single-earner couples spend more time watching TV together. 
E)  Reject if t > 2.485, t = 2.77, single-earner couples spend more time watching TV together. 
A)  Reject if t > 2.457, t = 2.59, single-earner couples spend more time watching TV together. 
B)  Reject if t > 2.508, t = 0.96, insufficient evidence to say that single-earner couples spend more time watching TV together. 
C)  Reject if t > 2.797, t = 2.57, single-earner couples spend more time watching TV together. 
D)  Reject if t > 2.042, t = 1.96, insufficient evidence to say that single-earner couples spend more time watching TV together. 
E)  Reject if t > 2.485, t = 2.77, single-earner couples spend more time watching TV together.

Question 14

If the null hypothesis that two means are equal is true, 97% of the computed z-values will lie between what two values?

Accepted Answer

A)  ±2.58 
B)  ±2.33 
C)  ±2.17 
D)  ±2.07 
E)  None of these statements are correct 
A)  ±2.58 
B)  ±2.33 
C)  ±2.17 
D)  ±2.07 
E)  None of these statements are correct

Question 15

To compare the effect of weather on sales of soft drinks, a soda manufacturer sampled two regions of the country with the following results. Is there a difference in sales between the 2 regions? 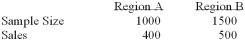  i. The null hypothesis is pa - pb = 0 ii. The alternate hypothesis is pa - pb > 0
Iii) The z-statistic is 3.57.

Accepted Answer

A)  (i), (ii) and (iii) are all correct statements 
B)  (i) and (ii) are correct statements, but not (iii). 
C)  (i) and (iii) are correct statements but not (ii). 
D)  (ii) and (iii) are correct statements but not (i). 
E)  (ii) is a correct statement, but not (i) and (iii). 
A)  (i), (ii) and (iii) are all correct statements 
B)  (i) and (ii) are correct statements, but not (iii). 
C)  (i) and (iii) are correct statements but not (ii). 
D)  (ii) and (iii) are correct statements but not (i). 
E)  (ii) is a correct statement, but not (i) and (iii).

Question 16

Of 150 adults who tried a new peach-flavoured peppermint patty, 81 rated it excellent. Of 200 children sampled, 123 rated it excellent. Using the 0.10 level of significance, can we conclude that there is a significant difference in the proportion of adults and the proportion of children who rate the new flavour as excellent? State the decision rule, the value of the test statistic, and your decision.

Accepted Answer

A) Reject if z > 1.645 or 1.645 or 1.96 or 1.96 or 1.645 or < -1.645, z = -1.41, no difference A) Reject if z > 1.645 or 1.645 or 1.96 or 1.96 or 1.645 or < -1.645, z = -1.41, no difference

Question 17

A national manufacturer of ball bearings is experimenting with two different processes for producing precision ball bearings. It is important that the diameters be as close as possible to an industry standard. The output from each process is sampled and the average error from the industry standard is calculated. The results are presented below.   The researcher is interested in determining whether there is evidence that the two processes yield different average errors. Ball Bearings
Hypothesis Test: Independent Groups (t-test, pooled variance)   What is the decision at the 1% level of significance?

Accepted Answer

A)  Reject the null hypothesis and conclude the means are different. 
B)  Reject the null hypothesis and conclude the means are the same. 
C)  Fail to reject the null hypothesis and conclude the means are the same. 
D)  Fail to reject the null hypothesis and conclude the means are different. 
E)  None of these statements are correct. 
A)  Reject the null hypothesis and conclude the means are different. 
B)  Reject the null hypothesis and conclude the means are the same. 
C)  Fail to reject the null hypothesis and conclude the means are the same. 
D)  Fail to reject the null hypothesis and conclude the means are different. 
E)  None of these statements are correct.

Question 18

i. If samples taken from two populations are not independent, then a test of paired differences is applied.
Ii) The paired difference test has (n1 + n2 - 2) degrees of freedom.
Iii) A statistics professor wants to compare grades of two different groups of students taking the same
Course in two different sections. This is an example of a paired sample.

Accepted Answer

A)  (i), (ii) and (iii) are all correct statements 
B)  (i) and (ii) are correct statements, but not (iii). 
C)  (i) is a correct statement, but not (ii) or (iii). 
D)  (ii) and (iii) are correct statements but not (i). 
E)  (ii) is a correct statement, but not (i) and (iii). 
A)  (i), (ii) and (iii) are all correct statements 
B)  (i) and (ii) are correct statements, but not (iii). 
C)  (i) is a correct statement, but not (ii) or (iii). 
D)  (ii) and (iii) are correct statements but not (i). 
E)  (ii) is a correct statement, but not (i) and (iii).

Question 19

Using two independent samples, two population means are compared to determine if a difference exists. The number in the first sample is fifteen and the number in the second sample is twelve. How many degrees of freedom are associated with the critical value?

Accepted Answer

A)  24 
B)  25 
C)  26 
D)  27 
E)  None of these statements is correct 
A)  24 
B)  25 
C)  26 
D)  27 
E)  None of these statements is correct

Question 20

The employees at the East Vancouver office of a multinational company are demanding higher salaries than those offered at the company office located in Oshawa Ontario. Their justification for the pay difference is that the difference between the average price of single-family houses in East Vancouver and that in Oshawa is more than $60,000. Before making a decision, the company management wants to study the difference in the prices of single-family houses for sale at the two locations.
The results of their search of recent house sales are as follows (in $000, rounded to the nearest thousand): 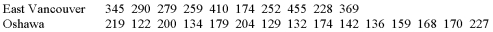  Assuming that the population distributions are approximately normal, can we conclude at the 0.05 significance level that the difference between the two population means is greater than $60,000? This example is what type of test?

Accepted Answer

A)  One sample test of means. 
B)  Two sample test of means. 
C)  Paired t-test. 
D)  Test of proportions. 
E)  None of these statements are correct 
A)  One sample test of means. 
B)  Two sample test of means. 
C)  Paired t-test. 
D)  Test of proportions. 
E)  None of these statements are correct

Administering the same test to a group of 15 students and a second group of 15 students to see which group scores higher is an example of:

i. If samples taken from two populations are not independent, then a test of paired differences is applied. Ii) The paired difference test has (n - 1) degrees of freedom. Iii) The paired t test is especially appropriate when the sample sizes of two groups are the same.

The results of a mathematics placement exam at Mercy College for two campuses is as follows: We want to test the hypothesis that the mean score on Campus 1 is higher than on Campus 2. Using the printout above, what decision(s) can be made?

If the null hypothesis that two means are equal is true, 97% of the computed z-values will lie between what two values?

Using two independent samples, two population means are compared to determine if a difference exists. The number in the first sample is fifteen and the number in the second sample is twelve. How many degrees of freedom are associated with the critical value?

What Is Statistics

Describing Data: Frequency Distributions and Graphic Presentation

Describing Data: Numerical Measures

A Survey of Probability Concepts

Discrete Probability Distributions

The Normal Probability Distribution

Sampling Methods and the Central Limit Theorem

Estimation and Confidence Intervals

One-Sample Tests of a Hypothesis

Analysis of Variance

Linear Regression and Correlation

Multiple Regression and Correlation Analysis

Chi-Square Applications for Nominal Data

Index Numbers

Time Series and Forecasting

An Introduction to Decision Theory

Filters

Exam 10: Two-Sample Tests of Hypothesis

Administering the same test to a group of 15 students and a second group of 15 students to see which group scores higher is an example of:

i. If samples taken from two populations are not independent, then a test of paired differences is applied. Ii) The paired difference test has (n - 1) degrees of freedom. Iii) The paired t test is especially appropriate when the sample sizes of two groups are the same.

The results of a mathematics placement exam at Mercy College for two campuses is as follows: We want to test the hypothesis that the mean score on Campus 1 is higher than on Campus 2. Using the printout above, what decision(s) can be made?

If the null hypothesis that two means are equal is true, 97% of the computed z-values will lie between what two values?

Using two independent samples, two population means are compared to determine if a difference exists. The number in the first sample is fifteen and the number in the second sample is twelve. How many degrees of freedom are associated with the critical value?

What Is Statistics

Describing Data: Frequency Distributions and Graphic Presentation

Describing Data: Numerical Measures

A Survey of Probability Concepts

Discrete Probability Distributions

The Normal Probability Distribution

Sampling Methods and the Central Limit Theorem

Estimation and Confidence Intervals

One-Sample Tests of a Hypothesis

Analysis of Variance

Linear Regression and Correlation

Multiple Regression and Correlation Analysis

Chi-Square Applications for Nominal Data

Index Numbers

Time Series and Forecasting

An Introduction to Decision Theory

Filters