Exam 9: One-Sample Tests of a Hypothesis
Exam 1: What Is Statistics78 Questions
Exam 2: Describing Data: Frequency Distributions and Graphic Presentation101 Questions
Exam 3: Describing Data: Numerical Measures186 Questions
Exam 4: A Survey of Probability Concepts121 Questions
Exam 5: Discrete Probability Distributions111 Questions
Exam 6: The Normal Probability Distribution129 Questions
Exam 7: Sampling Methods and the Central Limit Theorem78 Questions
Exam 8: Estimation and Confidence Intervals128 Questions
Exam 9: One-Sample Tests of a Hypothesis223 Questions
Exam 10: Two-Sample Tests of Hypothesis87 Questions
Exam 11: Analysis of Variance80 Questions
Exam 12: Linear Regression and Correlation150 Questions
Exam 13: Multiple Regression and Correlation Analysis98 Questions
Exam 14: Chi-Square Applications for Nominal Data113 Questions
Exam 15: Index Numbers65 Questions
Exam 16: Time Series and Forecasting86 Questions
Exam 17: An Introduction to Decision Theory37 Questions
Select questions type
To conduct a test of hypothesis with a small sample, we need to be able to make the following assumption that:
(Multiple Choice)
4.9/5  (42)
(42)
The mean weight of newborn infants at a community hospital is 6.6 pounds. A sample of seven infants is randomly selected and their weights at birth are recorded as 9.0, 7.3, 6.0, 8.8, 6.8, 8.4, and 6.6
Pounds. If α = 0.05, what is the critical t value?
(Multiple Choice)
4.8/5  (29)
(29)
A manufacturer claims that less than 1% of all his products do not meet the minimum government standards. A survey of 500 products revealed ten did not meet the standard. If the z-statistic is -1.96 and the level of significance is 0.01, what is your decision?
(Multiple Choice)
4.9/5  (34)
(34)
i. Two types of possible errors always exist when testing hypotheses-a Type I error, in which the null hypothesis is rejected when it should not have been rejected, and a Type II error in which the null hypothesis is not rejected when it should have been rejected.
Ii) A test statistic is a value determined from sample information collected to test the null hypothesis.
iii. The region or area of rejection defines the location of all those values that are so large or so small that the probability of their occurrence under a true null hypothesis is rather remote.
(Multiple Choice)
4.8/5  (37)
(37)
The mean gross annual incomes of certified tack welders are normally distributed with the mean of $50,000 and a standard deviation of $4,000. The ship building association wishes to find out whether their tack welders earn more or less than $50,000 annually. The alternate hypothesis is that the mean is not $50,000.
If the level of significance is 0.10, what is the decision rule?
(Multiple Choice)
4.8/5  (36)
(36)
One of the major U.S. tire makers wishes to review its warranty for their rainmaker tire. The warranty is for 40,000 miles. The tire company believes that the tire actually lasts more than 40,000 miles. A
Sample 49 tires revealed that the mean number of miles is 45,000 miles with a standard deviation of
15,000 miles. Test the hypothesis with a 0.05 significance level.
(Multiple Choice)
4.8/5  (37)
(37)
Given: null hypothesis is that the population mean is 16.9 against the alternative hypothesis that the population mean is not equal to 6.9. A random sample of 16 items results in a sample mean of 17.1 and the sample standard deviation is 2.4. It can be assumed that the population is normally distributed. Determine the observed "t" value.
(Multiple Choice)
4.8/5  (26)
(26)
What do we call the statement that determines if the null hypothesis is rejected?
(Multiple Choice)
4.7/5  (33)
(33)
The dean of a business school claims that the average starting salary of its graduates is more than $50,000. It is known that the population standard deviation is $10,000. Sample data on the starting salaries of 20 randomly selected recent graduates yielded a mean of $55,000. What is the value of the sample test statistic?
(Multiple Choice)
5.0/5  (31)
(31)
The dean of a business school claims that the average starting salary of its graduates is more than $50,000. It is known that the population standard deviation is $10,000. Sample data on the starting salaries of 25 randomly selected recent graduates yielded a mean of $52,000. What is the value of the sample test statistic?
(Multiple Choice)
4.7/5  (28)
(28)
What do tests of proportions require of both np and n(1 - p)?
(Multiple Choice)
4.7/5  (31)
(31)
What do we call the statement that determines if the null hypothesis is rejected?
(Multiple Choice)
4.7/5  (30)
(30)
For a two-tailed test at the 0.05 significance level, what is the rejection region when n if large?
(Multiple Choice)
4.7/5  (35)
(35)
i. To prevent bias, the level of significance is selected before setting up the decision rule and sampling the population.
Ii) The fifth and final step in testing a hypothesis is taking a sample and, based on the decision rule, deciding if the null hypothesis should be rejected.
Iii) When the null hypothesis is not rejected, the conclusion is that our sample data does not allow us to reject the null hypothesis.
(Multiple Choice)
4.8/5  (26)
(26)
i. To prevent bias, the level of significance is selected before setting up the decision rule and sampling the population.
Ii) The level of significance is the probability that a true hypothesis is rejected.
Iii) If the critical values of the test statistic z are ±1.96, they are the dividing points between the areas of rejection and non-rejection.
(Multiple Choice)
4.7/5  (32)
(32)
If 20 out of 50 students sampled live in a college dormitory, what is the estimated proportion of students at the University living in a dormitory?
(Multiple Choice)
4.9/5  (33)
(33)
If the alternate hypothesis states that μ does not equal 4,000, what is the rejection region for the hypothesis test?
(Multiple Choice)
4.8/5  (31)
(31)
i. The fifth and final step in testing a hypothesis is taking a sample and, based on the decision rule, deciding if the null hypothesis should be rejected.
ii. When the null hypothesis is not rejected, the conclusion is that our sample data does not allow us to reject the null hypothesis.
Iii) The level of significance is selected after setting up a decision rule and sampling the population.
(Multiple Choice)
4.8/5  (39)
(39)
Records on a fleet of trucks reveal that the average life of a set of spark plugs is normally distributed with a mean of 35,600 kilometres. A manufacturer of spark plugs claims that its plugs have an average life in excess of 35,600 kilometres. The fleet owner purchased 18 sets and found that the sample average life was 37,700 kilometres, the sample standard deviation was 2415 kilometres and the computed t = 3.677.
(Multiple Choice)
4.7/5  (31)
(31)
The mean gross annual incomes of certified tack welders are normally distributed with the mean of $50,000 and a standard deviation of $4,000. The ship building association wishes to find out whether their tack welders earn more or less than $50,000 annually. The alternate hypothesis is that the mean is not $50,000.
Given the following megastat printout, what conclusions can be made? 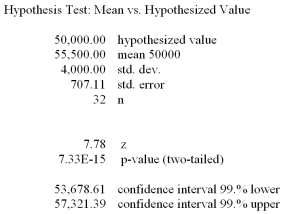
(Multiple Choice)
4.7/5  (35)
(35)
Showing 101 - 120 of 223
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)