Exam 9: One-Sample Tests of a Hypothesis
Exam 1: What Is Statistics78 Questions
Exam 2: Describing Data: Frequency Distributions and Graphic Presentation101 Questions
Exam 3: Describing Data: Numerical Measures186 Questions
Exam 4: A Survey of Probability Concepts121 Questions
Exam 5: Discrete Probability Distributions111 Questions
Exam 6: The Normal Probability Distribution129 Questions
Exam 7: Sampling Methods and the Central Limit Theorem78 Questions
Exam 8: Estimation and Confidence Intervals128 Questions
Exam 9: One-Sample Tests of a Hypothesis223 Questions
Exam 10: Two-Sample Tests of Hypothesis87 Questions
Exam 11: Analysis of Variance80 Questions
Exam 12: Linear Regression and Correlation150 Questions
Exam 13: Multiple Regression and Correlation Analysis98 Questions
Exam 14: Chi-Square Applications for Nominal Data113 Questions
Exam 15: Index Numbers65 Questions
Exam 16: Time Series and Forecasting86 Questions
Exam 17: An Introduction to Decision Theory37 Questions
Select questions type
A manufacturer claims that less than 1% of all his products do not meet the minimum government standards. A survey of 500 products revealed ten did not meet the standard.
(Multiple Choice)
4.8/5  (30)
(30)
What do tests of proportions require of both np and n(1 - p)?
(Multiple Choice)
4.9/5  (21)
(21)
i. A sample proportion is found by dividing the number of successes in the sample by the number sampled.
Ii) The standard normal distribution is the appropriate distribution when testing a hypothesis about a population proportion.
Iii) When testing population proportions, the z statistic can be used when np and n(1 - p) are greater than five.
(Multiple Choice)
4.8/5  (34)
(34)
A manufacturer claims that less than 1% of all his products do not meet the minimum government standards. A survey of 500 products revealed ten did not meet the standard. If the level of significance is 2%, what is the critical value is?
(Multiple Choice)
5.0/5  (47)
(47)
i. If the critical values of the test statistic z are ±1.96, they are the dividing points between the areas of rejection and non-rejection.
Ii) The probability of a Type I error is also referred to as alpha.
Iii) A Type I error is the probability of rejecting a true null hypothesis.
(Multiple Choice)
4.8/5  (42)
(42)
For a two-tailed test at the 0.05 significance level, what is the rejection region when n if large?
(Multiple Choice)
4.9/5  (38)
(38)
A manufacturer wants to increase the shelf life of a line of cake mixes. Past records indicate that the average shelf life of the mix is 216 days. After a revised mix has been developed, a sample of nine boxes of cake mix gave these shelf lives (in days): 215, 217, 218, 219, 216, 217, 217, 218 and 218. At the 0.025 level, has the shelf life of the cake mix increased?
(Multiple Choice)
4.7/5  (33)
(33)
i. An alternate hypothesis is a statement about a population parameter that is accepted when the null hypothesis is rejected.
Ii) The level of significance is the risk we assume of rejecting the null hypothesis when it is actually true.
Iii) The researcher must decide on the level of significance before formulating a decision rule and
Collecting sample data.
(Multiple Choice)
5.0/5  (31)
(31)
The mean weight of newborn infants at a community hospital is 6.6 pounds. A sample of seven infants is randomly selected and their weights at birth are recorded as 9.0, 7.3, 6.0, 8.8, 6.8, 8.4, and 6.6 pounds. What is the sample mean?
(Multiple Choice)
4.7/5  (33)
(33)
A nationwide survey of college students was conducted and found that students spend two hours per class hour studying. A professor at your school wants to determine whether the time students spend at your school is significantly different from the two hours. A random sample of fifteen statistics students is carried out and the findings indicate an average of 1.75 hours with a standard deviation of 0.24 hours.
(Multiple Choice)
4.8/5  (35)
(35)
The mean weight of newborn infants at a community hospital is 6.6 pounds. A sample of seven infants is randomly selected and their weights at birth are recorded as 9.0, 7.3, 6.0, 8.8, 6.8, 8.4, and 6.6 pounds. What are the degrees of freedom associated with this claim?
(Multiple Choice)
4.9/5  (31)
(31)
A manufacturer wants to increase the absorption capacity of a sponge. Based on past data, the average sponge could absorb 103.5ml. After the redesign, the absorption amounts of a sample of sponges were (in millilitres): 121.3, 109.2, 97.6, 103.5, 112.4, 115.3, 106.5, 112.4, 118.3, and 115.3. What is the decision rule at the 0.01 level of significance to test if the new design increased the absorption amount of the sponge?
(Multiple Choice)
4.8/5  (31)
(31)
The sample size and the population proportion are respectively represented by what symbols?
(Multiple Choice)
4.7/5  (41)
(41)
i. Two examples of a hypothesis are: 09 Key
1) mean monthly income from all sources for senior citizens is $841 and
2) twenty percent of juvenile offenders ultimately are caught and sentenced to prison.
Ii) Hypothesis testing is a procedure based on sample evidence and probability theory to decide whether the hypothesis is a reasonable statement.
Iii) Since there is more variability in sample means computed from smaller samples, we have more confidence in the resulting estimates and are less apt to reject null hypothesis.
(Multiple Choice)
4.9/5  (30)
(30)
A manufacturer claims that less than 1% of all his products do not meet the minimum government standards. A survey of 500 products revealed ten did not meet the standard.
(Multiple Choice)
5.0/5  (35)
(35)
The printout below refers to the weekly closing stock prices for Air Canada on 20 randomly selected weeks in 2000.  Using a 5% level of significance, can you say that the average Air Canada stock price was different from $19.50?
Using a 5% level of significance, can you say that the average Air Canada stock price was different from $19.50?
(Multiple Choice)
4.9/5  (36)
(36)
Given: null hypothesis is that the population mean is 16.9 against the alternative hypothesis that the population mean is not equal to 6.9. A random sample of 16 items results in a sample mean of 18.0
And the sample standard deviation is 2.4. It can be assumed that the population is normally distributed. Determine the observed "t" value.
(Multiple Choice)
4.8/5  (40)
(40)
A restaurant that bills its house account monthly is concerned that the average monthly bill exceeds $200 per account. A random sample of twelve accounts is selected, resulting in a sample mean of
$220 and a standard deviation of $12. The t-test is to be conducted at the 5% level of significance. The t-value is calculated to be 5.77. At the 0.01 level of significance, what is your decision?
(Multiple Choice)
4.8/5  (32)
(32)
The mean weight of newborn infants at a community hospital is 6.6 pounds. A sample of seven infants is randomly selected and their weights at birth are recorded as 9.0, 7.3, 6.0, 8.8, 6.8, 8.4, and 6.6 pounds. Does this sample support the original claim? What is the decision for a significant increase in the average birthrate at a 5% level of significance? 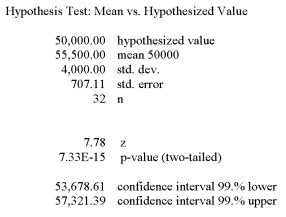
(Multiple Choice)
4.7/5  (41)
(41)
Showing 161 - 180 of 223
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)