Exam 4: Exponential and Logarithmic Functions

ng, in -Scientists often use a process called carbon dating to estimate the age of archaeological finds. The process measures the amount of carbon- 14 , a radioactive isotope with a half-life of 5,730 years. If sample of wood from an ancient artifact had 20 grams of carbon-14 initially, the amount remaining grams, is given by $A ( t ) = 20 \left( \frac { 1 } { 2 } \right) ^ { t / 5,730 }$ where $t$ is the number of years since the tree died. How many grams would be present after 5,730 years?

Solve the problem. -Sunlight is absorbed in water, and as a result the light intensity in oceans, lakes, and ponds decreases exponentially with depth. The percentage of visible light $P$ (in decimal form) at a depth of $x$ meters is given by $P = e ^ { - k x }$ , where $k$ is a constant related to the clarity and other physical properties of the water. The model for a particular lake is $P = e ^ { - 0.1284 x }$ . Determine the depth at which the light intensity is $80 \%$ of the value from the surface for this lake. Round to the nearest tenth of a meter.

Choose the one alternative that best completes the statement or answers the question. Solve the equation. - $5 ^ { 2 y } = 625$

Simplify the expression. - $\log _ { 1 / 5 } 625$

Simplify the expression without using a calculator. -log $10,000,000,000$

Determine if the statement is true or false. - $\log _ { 2 } ( 7 y ) + \log _ { 2 } 2 = \log _ { 2 } ( 7 y )$

Write the domain in interval notation. - $f ( x ) = \log ( 2 - x )$

Solve the equation. - $( \log x ) ^ { 2 } = \log x ^ { 2 }$

Evaluate the function at the given value of x. Round to 4 decimal places if necessary. - $f ( x ) = e ^ { x } ; f ( - 2 )$

Solve the equation. Write the solution set with the exact solutions. Also give approximate solutions to 4 decimal places if necessary. - $\log _ { 3 } \left( \log _ { 3 } x \right) = 0$

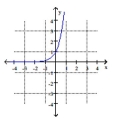
The graph of a function is given. Graph the inverse function. -

Simplify the expression. - $\ln e ^ { x ^ { 5 } + 4 }$

ng, in -A veterinarian depreciates a $\$ 10,000$ X-ray machine. He estimates that the resale value $V ( t )$ (in $\$$ ) after $t$ years is $90 \%$ of its value from the previous year. Therefore, the resale value can be approximated by $V ( t ) = 10,000 ( 0.9 ) ^ { t }$ . a. Find the resale value after $3 \mathrm { yr }$ . b. If the veterinarian wants to sell his practice $10 \mathrm { yr }$ after the X-ray machine was purchased, how much is the machine worth? Round to the nearest $\$ 100$ .

Solve the equation. Write the solution set with the exact solutions. Also give approximate solutions to 4 decimal places if necessary. - $\log ( p + 8 ) = 4.8$

Write the word or phrase that best completes each statement or answers the question. - $\log _ { 36 } 6 = \frac { 1 } { 2 }$

A one-to-one function is given. Write an expression for the inverse function. - $f ( x ) = 4 x ^ { 3 } - 9$

Solve the equation. Write the solution set with the exact solutions. Also give approximate solutions to 4 decimal places if necessary. - $\log _ { 7 } | x + 5 | = \log _ { 7 } 4$

Solve the equation. - $\log x + \log ( x - 11 ) = \log ( x - 35 )$

Write the domain in interval notation. - $f ( x ) = 14 - \frac { 1 } { \sqrt { 15 - x } }$

Write the logarithmic expression as a single logarithm with coefficient 1, and simplify as much as possible. - $\log _ { 5 } x - 8 \log _ { 5 } y - 9 \log _ { 5 } z$