Exam 4: Exponential and Logarithmic Functions
Exam 1: Equations and Inequalities296 Questions
Exam 2: Functions and Relations380 Questions
Exam 3: Polynomial and Rational Functions300 Questions
Exam 4: Exponential and Logarithmic Functions314 Questions
Exam 5: Systems of Equations and Inequalities215 Questions
Exam 6: Matrices and Determinants and Applications154 Questions
Exam 7: Analytic Geometry131 Questions
Exam 8: Sequences, Series, Induction, and Probability270 Questions
Exam 9: Review of Prerequisites226 Questions
Select questions type
Choose the one alternative that best completes the statement or answers the question.
Evaluate the function at the given value of x. Round to 4 decimal places if necessary.
-
(Multiple Choice)
4.8/5  (36)
(36)
Choose the one alternative that best completes the statement or answers the question.
Write the equation in exponential form.
-
(Multiple Choice)
4.9/5  (29)
(29)
A function defined by ) (is/is not) a one-to-one function if no horizontal line intersects the
graph of f in more than one point.
(Short Answer)
4.9/5  (41)
(41)
Solve the equation. Write the solution set with the exact solutions. Also give approximate solutions to 4
decimal places if necessary.
-
(Multiple Choice)
4.8/5  (35)
(35)
Solve the problem.
-The formula gives the loudness of sound (in ) based on the intensity of the sound (in ). The value is the minimal threshold for hearing for mid-frequency sounds. Hearing impairment is often measured according to the minimal sound level (in ) detected by an individual for sounds of various frequencies. If the minimum loudness of sound detected by an individual is , determine the corresponding intensity of sound.
(Multiple Choice)
4.9/5  (40)
(40)
Graph the points and from visual inspection, select the model that would best fit the data. Choose from y=mx+b (linear) y=a (exponential) y=a+bx (logarithmic) y= (logistic) Then use a graphing utility to find a function that fits the data. (Hint: For a logistic model, go to STAT, CALC,
Logistic.)
- x y 4 4.4 5 5.2 9 10.5 14 25.1 20 71.3 24 143.1
(Multiple Choice)
4.8/5  (35)
(35)
Determine if the relation defines y as a one-to-one function of x.
-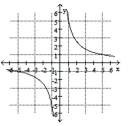
(Multiple Choice)
4.8/5  (35)
(35)
Solve the problem.
-Given that the domain of a one-to-one function is and the range of is , state the domain and range of .
(Multiple Choice)
4.9/5  (31)
(31)
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
- ــــــــــــــ.
(Short Answer)
4.9/5  (22)
(22)
Use transformations of the graph to graph the function. Write the domain and range in interval
notation.
-
(Multiple Choice)
4.9/5  (33)
(33)
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
- ـــــــــــــــــــ because .
(Short Answer)
4.9/5  (32)
(32)
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
-The domain of an exponential function is .
(Short Answer)
4.8/5  (35)
(35)
Graph the points and from visual inspection, select the model that would best fit the data. Choose from y=mx+b (linear) y=a (exponential) y=a+bx (logarithmic) y= (logistic) Then use a graphing utility to find a function that fits the data. (Hint: For a logistic model, go to STAT, CALC,
Logistic.)
- x y 10 41.2 20 47.5 30 51.2 40 53.8 50 55.9 60 57.5
(Multiple Choice)
4.8/5  (38)
(38)
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
- ــــــــــــــ
(Short Answer)
4.7/5  (35)
(35)
Showing 21 - 40 of 314
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)