Exam 4: Exponential and Logarithmic Functions
Exam 1: Equations and Inequalities296 Questions
Exam 2: Functions and Relations380 Questions
Exam 3: Polynomial and Rational Functions300 Questions
Exam 4: Exponential and Logarithmic Functions314 Questions
Exam 5: Systems of Equations and Inequalities215 Questions
Exam 6: Matrices and Determinants and Applications154 Questions
Exam 7: Analytic Geometry131 Questions
Exam 8: Sequences, Series, Induction, and Probability270 Questions
Exam 9: Review of Prerequisites226 Questions
Select questions type
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
-The range of an exponential function is .
(Short Answer)
4.8/5  (41)
(41)
Choose the one alternative that best completes the statement or answers the question.
Evaluate the function at the given value of x. Round to 4 decimal places if necessary.
-
(Multiple Choice)
4.8/5  (24)
(24)
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
-The equivalence property of logarithmic expressions indicates that if , then =
.
(Short Answer)
4.8/5  (37)
(37)
Use the change-of-base and a calculator to approximate the logarithm to 4 decimal places.
-
(Multiple Choice)
4.8/5  (39)
(39)
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
-The product property of logarithms indicates that ـــــــــــــfor positive real numbers , and where .
(Short Answer)
4.7/5  (29)
(29)
Solve the problem.
-Use the graph of to graph the function. Write the domain and range in interval notation.
(Multiple Choice)
4.8/5  (32)
(32)
Solve the problem.
-Use transformations of the graph of to graph the function.
(Multiple Choice)
4.9/5  (34)
(34)
Solve the problem.
-The millage rate is the amount of property tax per $1000 of the taxable value of a home. For a certain county the millage rate is 29 mil. A city within the county also imposes a flat fee of $101 per
Home. a. Write a function representing the total amount of property tax for a home with a taxable value thousand dollars.
b. Write an equation for .
c. What does the inverse function represent in the context of this problem?
(Multiple Choice)
4.8/5  (28)
(28)
Solve the problem.
-The atmospheric pressure on an object decreases as altitude increases. If a is the height (in km) above sea level, then the pressure P(a) (in mmHg) is approximated by P(a) = 760e-0.13a. Determine The atmospheric pressure at 7.176 km. Round to the nearest whole unit.
(Multiple Choice)
4.8/5  (27)
(27)
Write the word or phrase that best completes each statement or answers the question.
-
(Short Answer)
4.9/5  (33)
(33)
Choose the one alternative that best completes the statement or answers the question.
Solve for the indicated variable.
- for
(Multiple Choice)
4.9/5  (40)
(40)
Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
-The formula gives the amount A in an account after t years at an interest rate r under the
assumption that interest is compounded .
(Short Answer)
4.9/5  (42)
(42)
Solve the problem.
-The monthly costs for a small company to do business has been increasing over time in part due to inflation. The table gives the monthly cost y (in $) for the month of January for selected years. The Variable t represents the number of years since 2008.
Monthly Cost (Jan.) for Selected Years
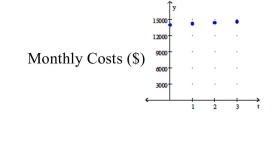 Year represents
a. Use a graphing utility to find a model of the form .
b. Write the function from part (a) as an exponential function with base .
c. Use the model to predict the monthly cost for January in the year 2,017 if this trend continues. Round to the nearest hundred dollars.
Year represents
a. Use a graphing utility to find a model of the form .
b. Write the function from part (a) as an exponential function with base .
c. Use the model to predict the monthly cost for January in the year 2,017 if this trend continues. Round to the nearest hundred dollars.
(Multiple Choice)
4.8/5  (35)
(35)
Solve the equation. Write the solution set with the exact solutions. Also give approximate solutions to 4
decimal places if necessary.
-
(Multiple Choice)
5.0/5  (38)
(38)
Write as the sum or difference of logarithms and fully simplify, if possible. Assume the variable
represents a positive real number.
-
(Multiple Choice)
4.7/5  (29)
(29)
Given the function f : = {(1, 2), (2, 3), (3, 4)} write the set of ordered pairs representing
(Short Answer)
4.8/5  (38)
(38)
Showing 181 - 200 of 314
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)