Exam 4: Exponential and Logarithmic Functions
Exam 1: Equations and Inequalities296 Questions
Exam 2: Functions and Relations380 Questions
Exam 3: Polynomial and Rational Functions300 Questions
Exam 4: Exponential and Logarithmic Functions314 Questions
Exam 5: Systems of Equations and Inequalities215 Questions
Exam 6: Matrices and Determinants and Applications154 Questions
Exam 7: Analytic Geometry131 Questions
Exam 8: Sequences, Series, Induction, and Probability270 Questions
Exam 9: Review of Prerequisites226 Questions
Select questions type
Use the quotient property of logarithms to write the logarithm as a difference of logarithms. Then
simplify if possible.
-
(Multiple Choice)
4.8/5  (30)
(30)
Choose the one alternative that best completes the statement or answers the question.
Solve for the indicated variable.
- for
(Multiple Choice)
4.9/5  (36)
(36)
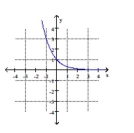
The graph of a function is given. Graph the inverse function.
-
(Multiple Choice)
4.9/5  (38)
(38)
Use the change-of-base and a calculator to approximate the logarithm to 4 decimal places.
-
(Multiple Choice)
4.8/5  (33)
(33)
Write the word or phrase that best completes each statement or answers the question.
-
(Multiple Choice)
4.8/5  (38)
(38)
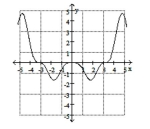
Determine if the relation defines y as a one-to-one function of x.
-
(Multiple Choice)
4.8/5  (34)
(34)
Write the logarithm as a sum or difference of logarithms. Simplify each term as much as possible.
-
(Multiple Choice)
4.9/5  (38)
(38)
ng, in
-The population of bacteria culture was 2000 at noon, and was increasing at a rate of per hour. The number can be found using the function
where is the number of hours past noon. Predict the population 11 hours later, at to the nearest whole number.
(Multiple Choice)
4.8/5  (29)
(29)
A one-to-one function is given. Write an expression for the inverse function.
-
(Multiple Choice)
4.8/5  (44)
(44)
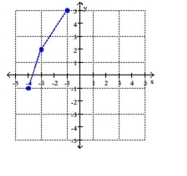
The graph of a function is given. Graph the inverse function.
-
(Multiple Choice)
4.9/5  (36)
(36)
A one-to-one function is given. Write an expression for the inverse function.
-
(Multiple Choice)
4.9/5  (36)
(36)
Write the logarithmic expression as a single logarithm with coefficient 1, and simplify as much as
possible.
-
(Multiple Choice)
4.7/5  (40)
(40)
Write the logarithmic expression as a single logarithm with coefficient 1, and simplify as much as
possible.
-
(Multiple Choice)
4.7/5  (36)
(36)
Graph the function and write the domain and range in interval notation.
-
(Multiple Choice)
4.8/5  (33)
(33)
Choose the one alternative that best completes the statement or answers the question.
Solve for the indicated variable.
- for
(Multiple Choice)
4.7/5  (38)
(38)
Solve the problem.
-A bond grows to in 8 yr under continuous compounding. Find the interest rate. Round our answer to the nearest whole percent.
(Multiple Choice)
4.8/5  (37)
(37)
Showing 121 - 140 of 314
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)