Question 1

Determine if the statement is true or false.
-$\log ( x y ) - ( \log x ) ( \log y )$

Accepted Answer

A) True 
 B)False

Question 2

Solve the equation. Write the solution set with the exact values given in terms of natural or common
logarithms. Also give approximate solutions to 4 decimal places, if necessary.
-$$e ^ { 7 x } = - 9 e ^ { 2 x }$$

Accepted Answer

A)  $\left\{ \frac { \ln 9 } { 5 } \right\} ; x \approx 2.2756$ 
B)  $\left\{ \frac { \ln - 9 } { 5 } \right\} ; x \approx 2.2756$ 
C)  $\left\{ \frac { \ln 9 } { - 5 } \right\} ; x \approx - 2.2756$ 
D)  \{ \} 
A)  $\left\{ \frac { \ln 9 } { 5 } \right\} ; x \approx 2.2756$ 
B)  $\left\{ \frac { \ln - 9 } { 5 } \right\} ; x \approx 2.2756$ 
C)  $\left\{ \frac { \ln 9 } { - 5 } \right\} ; x \approx - 2.2756$ 
D)  \{ \}

Question 3

Apply the power property of logarithms.
-$$\log ( 2 t - 7 ) ^ { 3 }$$

Accepted Answer

A)  $3 \log 2 \cdot 3 \log t - 3 \log 7$ 
B)  $3 \log 2 + 3 \log t - 3 \log 7$ 
C)  $3 \log 2 t - 3 \log 7$ 
D)  $3 \log ( 2 t - 7 )$ 
A)  $3 \log 2 \cdot 3 \log t - 3 \log 7$ 
B)  $3 \log 2 + 3 \log t - 3 \log 7$ 
C)  $3 \log 2 t - 3 \log 7$ 
D)  $3 \log ( 2 t - 7 )$

Question 4

Solve the problem.
-A new teaching method to teach vocabulary to sixth-graders involves having students work in groups on an assignment to learn new words. After the lesson was completed, the students were tested at 1-month intervals. The average score for the class $S ( t )$ can be modeled by
$$S ( t ) = 96 - 10 \ln ( t + 1 )$$ where t is the time in months after completing the assignment. If the average score is 73, how many
months had passed since the students completed the assignment? 
A) 11 months
B) 9 months
C) 12 months
D) 7 months

Accepted Answer

The answer of Solve the problem.
-A new teaching method to...

Question 5

Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
-$$\text { A function defined by } y = a b ^ { x } \text { can be written in terms of an exponential function base } e \text { as }$$________

Accepted Answer

The answer of Write the word or phrase that best...

Question 6

Solve the problem.
-The number n of monthly payments of P dollars each required to pay off a loan of A dollars in its entirety at interest rate r is given by $$n = - \frac { \log \left( 1 - \frac { A r } { 12 P } \right) } { \log \left( 1 + \frac { r } { 12 } \right) }$$ A college student wants to buy a car and realizes that he can only afford payments of $180 per month. If he
Borrows $5,000 at 6% interest and pays it off, how many months will it take him to retire the loan?
Round to the nearest month.

Accepted Answer

A)  30 months 
B)  28 months 
C)  29 months 
D)  31 months 
A)  30 months 
B)  28 months 
C)  29 months 
D)  31 months

Question 7

Write the equation in logarithmic form.
-$$3 ^ { 5 } = 243$$

Accepted Answer

A)  $\log _ { 243 } 5 = 3$ 
B)  $\log _ { 3 } 243 = 5$ 
C)  $\log _ { 243 } 3 = 5$ 
D)  $\log _ { 5 } 243 = 3$ 
A)  $\log _ { 243 } 5 = 3$ 
B)  $\log _ { 3 } 243 = 5$ 
C)  $\log _ { 243 } 3 = 5$ 
D)  $\log _ { 5 } 243 = 3$

Question 8

A one-to-one function is given. Write an expression for the inverse function.
-$$f ( x ) = \frac { x + 8 } { x + 6 }$$

Accepted Answer

A)  $f ^ { - 1 } ( x ) = \frac { x - 6 } { x - 8 }$ 
B)  $f ^ { - 1 } ( x ) = \frac { x + 6 } { x + 8 }$ 
C)  $f ^ { - 1 } ( x ) = \frac { 8 + 6 x } { x + 1 }$ 
D)  $f ^ { - 1 } ( x ) = \frac { 8 - 6 x } { x - 1 }$ 
A)  $f ^ { - 1 } ( x ) = \frac { x - 6 } { x - 8 }$ 
B)  $f ^ { - 1 } ( x ) = \frac { x + 6 } { x + 8 }$ 
C)  $f ^ { - 1 } ( x ) = \frac { 8 + 6 x } { x + 1 }$ 
D)  $f ^ { - 1 } ( x ) = \frac { 8 - 6 x } { x - 1 }$

Question 9

Choose the one alternative that best completes the statement or answers the question.
Use the product property of logarithms to write the logarithm as a sum of logarithms. Then simplify if
possible.
-$$\log _ { 9 } [ ( 17 + t ) \cdot u ]$$

Accepted Answer

A)  $\left. \left. \log _ { 9 } ( 17 + t ) + \log _ { 9 } u \right) \right]$ 
B)  $\log _ { 9 } 17 + \log _ { 9 } t \cdot \log _ { 9 } u$ 
C)  $\left( \log _ { 9 } 17 + \log _ { 9 } t \right) \cdot \log _ { 9 } u$ 
D)  $\log _ { 9 } 17 \cdot \log _ { 9 } t + \log _ { 9 } u$ 
A)  $\left. \left. \log _ { 9 } ( 17 + t ) + \log _ { 9 } u \right) \right]$ 
B)  $\log _ { 9 } 17 + \log _ { 9 } t \cdot \log _ { 9 } u$ 
C)  $\left( \log _ { 9 } 17 + \log _ { 9 } t \right) \cdot \log _ { 9 } u$ 
D)  $\log _ { 9 } 17 \cdot \log _ { 9 } t + \log _ { 9 } u$

Question 10

Write the word or phrase that best completes each statement or answers the question.
Provide the missing information.
-The ــــــــ property of logarithms indicates that $\log _ { b } \left( \frac { x } { y } \right) =$ ـــــــــــــــ for positive real numbers $b , x$, and $y$ where $b \neq 1$.

Accepted Answer

The answer of Write the word or phrase that best...

Question 11

Solve the problem.
-The sales of a book tend to increase over the short-term as word-of-mouth makes the book "catch on." The number of books sold N(t) for a new novel t weeks after release at a certain book store is given In the table for the first 6 weeks. 
$\begin{array}{c|c}
\text { Weeks } t & \begin{array}{c}
\text { Number } \
\text { Sold } N(t)
\end{array} \
\hline 1 & 20 \
2 & 28 \
3 & 33 \
4 & 36 \
5 & 38 \
6 & 41
\end{array}$

Book Sales vs. Weeks After Release

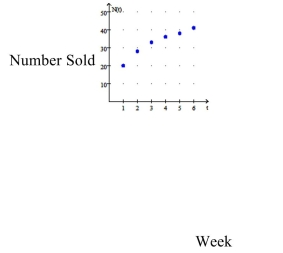a. Find a model of the form $y = a + b \ln t$.
b. Use the model to predict the sales in week 11. Round to the nearest whole unit.
c. Is it reasonable to assume that the logarithmic trend will continue? Why or why not?

Accepted Answer

A)  a. $y = 3.9 + 19 \ln t$
b. 49 books
c. Yes. The number of books sold will continue to increase although the sales will approach a limit. 
B)  a. $y = 20.1 + 11.5 \ln t$
b. 48 books
c. Yes. The number of books sold will continue to increase although the sales will approach a limit. 
C)  a. $y = 3.9 + 19 \ln t$
b. 49 books
c. No. The trend cannot continue indefinitely. At some point, book sales will begin to decrease as most reading enthusiasts have read the book. 
D)  a. $y = 20.1 + 11.5 \ln t$
b. 48 books
c. No. The trend cannot continue indefinitely. At some point, book sales will begin to decrease as most reading enthusiasts have read the book. 
A)  a. $y = 3.9 + 19 \ln t$
b. 49 books
c. Yes. The number of books sold will continue to increase although the sales will approach a limit. 
B)  a. $y = 20.1 + 11.5 \ln t$
b. 48 books
c. Yes. The number of books sold will continue to increase although the sales will approach a limit. 
C)  a. $y = 3.9 + 19 \ln t$
b. 49 books
c. No. The trend cannot continue indefinitely. At some point, book sales will begin to decrease as most reading enthusiasts have read the book. 
D)  a. $y = 20.1 + 11.5 \ln t$
b. 48 books
c. No. The trend cannot continue indefinitely. At some point, book sales will begin to decrease as most reading enthusiasts have read the book.

Question 12

Solve the problem.
-After a new product is launched the cumulative sales $S ( t )$ (in $\$ 1000$ ) $t$ weeks after launch is given by:
$$S ( t ) = \frac { 74 } { 1 + 14 e ^ { - 0.4 t } }$$
Determine the cumulative amount in sales 4 weeks after launch. Round to the nearest thousand.

Accepted Answer

A)  $\$ 19,000$ 
B)  $\$ 1,000$ 
C)  $\$ 55,000$ 
D)  $\$ 10,000$ 
A)  $\$ 19,000$ 
B)  $\$ 1,000$ 
C)  $\$ 55,000$ 
D)  $\$ 10,000$

Question 13

Write the equation in logarithmic form.
-$$8 ^ { 2 } = b$$

Accepted Answer

A)  $\log _ { b } 8 = 2$ 
B)  $\log _ { b } 2 = 8$ 
C)  $\log _ { 2 } b = 8$ 
D)  $\log _ { 8 } b = 2$ 
A)  $\log _ { b } 8 = 2$ 
B)  $\log _ { b } 2 = 8$ 
C)  $\log _ { 2 } b = 8$ 
D)  $\log _ { 8 } b = 2$

Question 14

Solve the problem.
-If $\$ 22,000$ is invested in an account earning $4.5 \%$ interest compounded continuously, determine how long it will take the money to quadruple. Round to the nearest year. Use the model $A = P e ^ { r t }$ where $A$ represents the future value of $P$ dollars invested at an interest rate $r$ compounded continuously for $t$ years.

Accepted Answer

A)  3 years 
B)  308 years 
C)  31 years 
D)  36 years 
A)  3 years 
B)  308 years 
C)  31 years 
D)  36 years

Question 15

Choose the one alternative that best completes the statement or answers the question.
Solve for the indicated variable.
-$\log E - 12.8 = 1.41 M$ for $E$

Accepted Answer

A)  $E = 10 ^ { 9.08 M }$ 
B)  $E = 10 ^ { 1.41 M - 12.8 }$ 
C)  $E = 10 ^ { 1.41 M } + 12.8$ 
D)  $E = 10 ^ { 1.41 M + 12.8 }$ 
A)  $E = 10 ^ { 9.08 M }$ 
B)  $E = 10 ^ { 1.41 M - 12.8 }$ 
C)  $E = 10 ^ { 1.41 M } + 12.8$ 
D)  $E = 10 ^ { 1.41 M + 12.8 }$

Question 16

Choose the one alternative that best completes the statement or answers the question.
Solve the equation.
-$$\left( \frac { 3 } { 4 } \right) ^ { 4 y + 6 } = \left( \frac { 9 } { 16 } \right) ^ { 5 y }$$

Accepted Answer

A)  $\{ 0 \}$ 
B)  $\{ 4 \}$ 
C)  $\{ 1 \}$ 
D)  No real solution 
A)  $\{ 0 \}$ 
B)  $\{ 4 \}$ 
C)  $\{ 1 \}$ 
D)  No real solution

Question 17

Approximate the value of the logarithm to four decimal places.
-$\log \left( 6.8 \cdot 10 ^ { - 19 } \right)$

Accepted Answer

A)  -19.1675 
B)  -18.1675 
C)  -20.1675 
D)  -17.1675 
A)  -19.1675 
B)  -18.1675 
C)  -20.1675 
D)  -17.1675

Question 18

Choose the one alternative that best completes the statement or answers the question.
Solve for the indicated variable.
-$L = 10 \log \left( \frac { I } { I _ { 0 } } \right)$ for $I$

Accepted Answer

A)  $I = I _ { 0 } 10 ^ { ( L - 10 ) }$ 
B)  $I = I _ { 0 } - 10 ^ { ( L / 10 ) }$ 
C)  $I = I _ { 0 } 10 ^ { L }$ 
D)  $I = I _ { 0 } 10 ^ { ( L / 10 ) }$ 
A)  $I = I _ { 0 } 10 ^ { ( L - 10 ) }$ 
B)  $I = I _ { 0 } - 10 ^ { ( L / 10 ) }$ 
C)  $I = I _ { 0 } 10 ^ { L }$ 
D)  $I = I _ { 0 } 10 ^ { ( L / 10 ) }$

Question 19

Determine whether the two functions are inverses.
-$$f ( x ) = \frac { 2 } { x + 3 } \text { and } g ( x ) = \frac { 2 + 3 x } { x }$$

Accepted Answer

A)  Yes 
B)  No 
A)  Yes 
B)  No

Question 20

Solve the equation.
-$$\log _ { 3 } t + \log _ { 3 } ( t + 2 ) = \log _ { 3 } 80$$

Accepted Answer

A)  $\{ 39 \}$ 
B)  $\{ 10 \}$ 
C)  $\{ 8 \}$ 
D)  $\{ - 10,8 \}$ 
A)  $\{ 39 \}$ 
B)  $\{ 10 \}$ 
C)  $\{ 8 \}$ 
D)  $\{ - 10,8 \}$

Determine if the statement is true or false. - $\log ( x y ) - ( \log x ) ( \log y )$

Solve the equation. Write the solution set with the exact values given in terms of natural or common logarithms. Also give approximate solutions to 4 decimal places, if necessary. - $e ^ { 7 x } = - 9 e ^ { 2 x }$

Apply the power property of logarithms. - $\log ( 2 t - 7 ) ^ { 3 }$

Write the word or phrase that best completes each statement or answers the question. Provide the missing information. - $\text { A function defined by } y = a b ^ { x } \text { can be written in terms of an exponential function base } e \text { as }$ ________

Write the equation in logarithmic form. - $3 ^ { 5 } = 243$

A one-to-one function is given. Write an expression for the inverse function. - $f ( x ) = \frac { x + 8 } { x + 6 }$

Choose the one alternative that best completes the statement or answers the question. Use the product property of logarithms to write the logarithm as a sum of logarithms. Then simplify if possible. - $\log _ { 9 } [ ( 17 + t ) \cdot u ]$

Solve the problem. -After a new product is launched the cumulative sales $S ( t )$ (in $\$ 1000$ ) $t$ weeks after launch is given by: $S ( t ) = \frac { 74 } { 1 + 14 e ^ { - 0.4 t } }$ Determine the cumulative amount in sales 4 weeks after launch. Round to the nearest thousand.

Write the equation in logarithmic form. - $8 ^ { 2 } = b$

Choose the one alternative that best completes the statement or answers the question. Solve for the indicated variable. - $\log E - 12.8 = 1.41 M$ for $E$

Choose the one alternative that best completes the statement or answers the question. Solve the equation. - $\left( \frac { 3 } { 4 } \right) ^ { 4 y + 6 } = \left( \frac { 9 } { 16 } \right) ^ { 5 y }$

Approximate the value of the logarithm to four decimal places. - $\log \left( 6.8 \cdot 10 ^ { - 19 } \right)$

Choose the one alternative that best completes the statement or answers the question. Solve for the indicated variable. - $L = 10 \log \left( \frac { I } { I _ { 0 } } \right)$ for $I$

Determine whether the two functions are inverses. - $f ( x ) = \frac { 2 } { x + 3 } \text { and } g ( x ) = \frac { 2 + 3 x } { x }$

Solve the equation. - $\log _ { 3 } t + \log _ { 3 } ( t + 2 ) = \log _ { 3 } 80$

Equations and Inequalities

Functions and Relations

Polynomial and Rational Functions

Systems of Equations and Inequalities

Matrices and Determinants and Applications

Analytic Geometry

Sequences, Series, Induction, and Probability

Review of Prerequisites

Filters

Exam 4: Exponential and Logarithmic Functions

Determine if the statement is true or false. - log⁡(xy)−(log⁡x)(log⁡y)\log ( x y ) - ( \log x ) ( \log y )log(xy)−(logx)(logy)

Solve the equation. Write the solution set with the exact values given in terms of natural or common logarithms. Also give approximate solutions to 4 decimal places, if necessary. - e7x=−9e2xe ^ { 7 x } = - 9 e ^ { 2 x }e7x=−9e2x

Apply the power property of logarithms. - log⁡(2t−7)3\log ( 2 t - 7 ) ^ { 3 }log(2t−7)3

Write the equation in logarithmic form. - 35=2433 ^ { 5 } = 24335=243

A one-to-one function is given. Write an expression for the inverse function. - f(x)=x+8x+6f ( x ) = \frac { x + 8 } { x + 6 }f(x)=x+6x+8​

Choose the one alternative that best completes the statement or answers the question. Use the product property of logarithms to write the logarithm as a sum of logarithms. Then simplify if possible. - log⁡9[(17+t)⋅u]\log _ { 9 } [ ( 17 + t ) \cdot u ]log9​[(17+t)⋅u]

Write the equation in logarithmic form. - 82=b8 ^ { 2 } = b82=b

Choose the one alternative that best completes the statement or answers the question. Solve for the indicated variable. - log⁡E−12.8=1.41M\log E - 12.8 = 1.41 MlogE−12.8=1.41M for EEE

Choose the one alternative that best completes the statement or answers the question. Solve the equation. - (34)4y+6=(916)5y\left( \frac { 3 } { 4 } \right) ^ { 4 y + 6 } = \left( \frac { 9 } { 16 } \right) ^ { 5 y }(43​)4y+6=(169​)5y

Approximate the value of the logarithm to four decimal places. - log⁡(6.8⋅10−19)\log \left( 6.8 \cdot 10 ^ { - 19 } \right)log(6.8⋅10−19)

Choose the one alternative that best completes the statement or answers the question. Solve for the indicated variable. - L=10log⁡(II0)L = 10 \log \left( \frac { I } { I _ { 0 } } \right)L=10log(I0​I​) for III

Determine whether the two functions are inverses. - f(x)=2x+3 and g(x)=2+3xxf ( x ) = \frac { 2 } { x + 3 } \text { and } g ( x ) = \frac { 2 + 3 x } { x }f(x)=x+32​ and g(x)=x2+3x​

Solve the equation. - log⁡3t+log⁡3(t+2)=log⁡380\log _ { 3 } t + \log _ { 3 } ( t + 2 ) = \log _ { 3 } 80log3​t+log3​(t+2)=log3​80