Exam 2: Linear and Quadratic Functions
Exam 1: Functions and Their Graphs297 Questions
Exam 2: Linear and Quadratic Functions302 Questions
Exam 3: Polynomial and Rational Functions354 Questions
Exam 4: Exponential and Logarithmic Functions517 Questions
Exam 5: Trigonometric Functions354 Questions
Exam 6: Analytic Trigonometry342 Questions
Exam 7: Applications of Trigonometric Functions105 Questions
Exam 8: Polar Coordinates; Vectors253 Questions
Exam 9: Analytic Geometry200 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability115 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Foundations: a Prelude to Functions234 Questions
Exam 15: Graphing Utilities29 Questions
Select questions type
Solve the problem.
-An open box is to be constructed from a square sheet of plastic by removing a square of side 4 inches from each corner, and then turning up the sides. If the box must have a volume of 1,600 cubic inches, find the length of one
Side of the open box.
(Multiple Choice)
4.9/5  (31)
(31)
Find the real zeros, if any, of each quadratic function using the quadratic formula. List the x-intercepts, if any, of the
graph of the function.
-
(Multiple Choice)
4.7/5  (31)
(31)
Choose the one alternative that best completes the statement or answers the question.
-Alan is building a garden shaped like a rectangle with a semicircle attached to one short side. If he has 40 feet of fencing to go around it, what dimensions will give him the maximum area in the garden?
(Multiple Choice)
4.7/5  (35)
(35)
Solve the inequality. Express your answer using interval notation. Graph the solution set.
-

(Multiple Choice)
5.0/5  (31)
(31)
Solve the problem.
-The manufacturer of a CD player has found that the revenue R (in dollars) is when the unit price is p dollars. If the manufacturer sets the price p to maximize revenue, what is the maximum revenue to the nearest whole dollar?
(Multiple Choice)
4.9/5  (41)
(41)
Solve the inequality. Express your answer using interval notation. Graph the solution set.
-

(Multiple Choice)
4.8/5  (31)
(31)
Determine the quadratic function whose graph is given.
-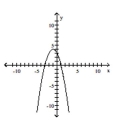 Vertex:
-intercept:
Vertex:
-intercept:
(Multiple Choice)
4.9/5  (28)
(28)
Use a graphing utility to find the equation of the line of best fit. Round to two decimal places, if necessary.
- x 10 20 30 40 50 y 3.9 4.6 5.4 6.9 8.3
(Multiple Choice)
4.8/5  (38)
(38)
Use the slope and y-intercept to graph the linear function.
-
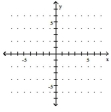
(Multiple Choice)
4.9/5  (39)
(39)
Solve the problem.
-The length of a vegetable garden is 3 feet longer than its width. If the area of the garden is 130 square feet, find its dimensions.
(Multiple Choice)
4.8/5  (32)
(32)
Determine, without graphing, whether the given quadratic function has a maximum value or a minimum value and then
find that value.
-
(Multiple Choice)
4.8/5  (39)
(39)
Find the vertex and axis of symmetry of the graph of the function.
-
(Multiple Choice)
4.8/5  (32)
(32)
Determine where the function is increasing and where it is decreasing.
-
(Multiple Choice)
4.8/5  (30)
(30)
employees each year.
Choose the one alternative that best completes the statement or answers the question.
Use factoring to find the zeros of the quadratic function. List the x-intercepts of the graph of the function.
-
(Multiple Choice)
4.7/5  (30)
(30)
Graph the function f by starting with the graph of y = x2 and using transformations (shifting, compressing, stretching,
and/or reflection).
-
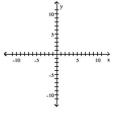
(Multiple Choice)
4.8/5  (28)
(28)
Solve f(x) = g(x). Find the points of intersection of the graphs of the two functions.
- f(x)=7x+8 g(x)=
(Multiple Choice)
4.7/5  (23)
(23)
Showing 61 - 80 of 302
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)