Exam 3: Polynomial and Rational Functions
Exam 1: Functions and Their Graphs301 Questions
Exam 2: Linear and Quadratic Functions301 Questions
Exam 3: Polynomial and Rational Functions350 Questions
Exam 4: Exponential and Logarithmic Functions518 Questions
Exam 5: Trigonometric Functions366 Questions
Exam 6: Analytic Trigonometry402 Questions
Exam 7: Applications of Trigonometric Functions103 Questions
Exam 8: Polar Coordinates; Vectors270 Questions
Exam 9: Analytic Geometry197 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability108 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Review228 Questions
Select questions type
Solve the problem.
-Determine which rational function has a graph that crosses the -axis at , touches the -axis at , has vertical asymptotes at and , and has one horizontal asymptote at .
(Multiple Choice)
4.9/5  (36)
(36)
Solve the problem.
-Decide which of the rational functions might have the given graph. 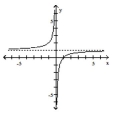 A)
B)
C)
D)
A)
B)
C)
D)
(Multiple Choice)
4.8/5  (40)
(40)
Use the given zero to find the remaining zeros of the function.
- ; zero:
(Multiple Choice)
4.8/5  (42)
(42)
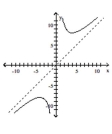
Use the graph to find the vertical asymptotes, if any, of the function.
-
(Multiple Choice)
4.7/5  (39)
(39)
State whether the function is a polynomial function or not. If it is, give its degree. If it is not, tell why not.
-
(Multiple Choice)
4.8/5  (45)
(45)
Analyze the graph of the given function f as follows:
(a) Determine the end behavior: find the power function that the graph of f resembles for large values of | (b) Find the x- and y-intercepts of the graph.
(c) Determine whether the graph crosses or touches the x-axis at each x-intercept.
(d) Graph f using a graphing utility.
(e) Use the graph to determine the local maxima and local minima, if any exist. Round turning points to two decimal places.
(f) Use the information obtained in (a) - (e) to draw a complete graph of f by hand. Label all intercepts and turning points.
(g) Find the domain of f. Use the graph to find the range of f.
(h) Use the graph to determine where f is increasing and where f is decreasing.
-
(Essay)
4.8/5  (31)
(31)
Use the Factor Theorem to determine whether x - c is a factor of f. If it is, write f in factored form, that is, write f in the
form f(x) = (x - c)(quotient).
-
(Multiple Choice)
4.8/5  (36)
(36)
Find the indicated intercept(s) of the graph of the function.2133:2139
-
(Multiple Choice)
4.9/5  (33)
(33)
List the potential rational zeros of the polynomial function. Do not find the zeros.
-
(Multiple Choice)
4.8/5  (43)
(43)
Find the indicated intercept(s) of the graph of the function.2133:2139
- -intercept of
(Multiple Choice)
4.8/5  (32)
(32)
Use transformations of the graph o to graph the function.
-
 A)
A)
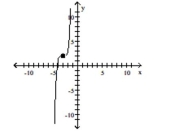 B)
B)
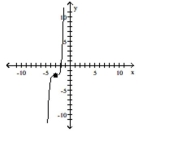 C)
C)
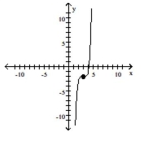 D)
D)
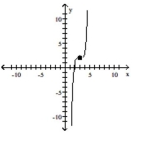
(Multiple Choice)
4.9/5  (39)
(39)
The equation has a solution r in the interval indicated. Approximate this solution correct to two decimal places.
-
(Short Answer)
4.7/5  (40)
(40)
List the potential rational zeros of the polynomial function. Do not find the zeros.
-
(Multiple Choice)
4.9/5  (40)
(40)
Information is given about a polynomial f(x) whose coefficients are real numbers. Find the remaining zeros of f.
-Degree 3; zeros:
(Multiple Choice)
4.9/5  (38)
(38)
Solve the problem.
-The acceleration due to gravity g (in meters per second per second) at a height h meters above sea level is given
by where is the radius of Earth in meters. Death Valley in California is 86 m
below sea level.
a) Find the value of g(h) at Death Valley to four decimal places.
b) Compare the value in (a) to the value of g(h) at sea level.
(Essay)
4.8/5  (31)
(31)
Find the indicated intercept(s) of the graph of the function.2133:2139
- -intercept of
(Multiple Choice)
4.9/5  (35)
(35)
Showing 321 - 340 of 350
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)