Exam 3: Polynomial and Rational Functions
Exam 1: Functions and Their Graphs301 Questions
Exam 2: Linear and Quadratic Functions301 Questions
Exam 3: Polynomial and Rational Functions350 Questions
Exam 4: Exponential and Logarithmic Functions518 Questions
Exam 5: Trigonometric Functions366 Questions
Exam 6: Analytic Trigonometry402 Questions
Exam 7: Applications of Trigonometric Functions103 Questions
Exam 8: Polar Coordinates; Vectors270 Questions
Exam 9: Analytic Geometry197 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability108 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Review228 Questions
Select questions type
Find the indicated intercept(s) of the graph of the function.2133:2139
-
(Multiple Choice)
4.8/5  (39)
(39)
Form a polynomial whose zeros and degree are given. Use a leading coefficient of 1.
-Zeros: -3, -2, 3; degree 3 A)
B)
C)
D)
(Multiple Choice)
4.8/5  (36)
(36)
Use the graph to determine the domain and range of the function.
- A) domain:
range: or
B) domain: all real numbers
range: or
C) domain: or
range:
D) domain:
range: all real numbers
A) domain:
range: or
B) domain: all real numbers
range: or
C) domain: or
range:
D) domain:
range: all real numbers
(Multiple Choice)
4.9/5  (50)
(50)
Use transformations of the graph o to graph the function.
-
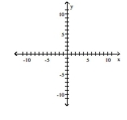 A)
A)
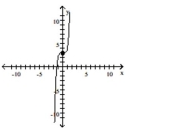 B)
B)
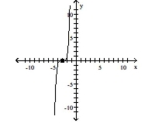 C)
C)
 D)
D)

(Multiple Choice)
4.8/5  (38)
(38)
Form a polynomial whose zeros and degree are given. Use a leading coefficient of 1.
-Zeros: -5, multiplicity 2; -1, multiplicity 1; degree 3 A)
B)
C)
D)
(Multiple Choice)
4.9/5  (44)
(44)
Information is given about a polynomial f(x) whose coefficients are real numbers. Find the remaining zeros of f.
-Degree 4; zeros: ,
(Multiple Choice)
4.7/5  (33)
(33)
Find the indicated intercept(s) of the graph of the function.2133:2139
- -intercept of
(Multiple Choice)
4.8/5  (31)
(31)
Use transformations of the graph o to graph the function.
-
 A)
A)
 B)
B)
 C)
C)
 D)
D)

(Multiple Choice)
4.9/5  (37)
(37)
Analyze the graph of the given function f as follows:
(a) Determine the end behavior: find the power function that the graph of f resembles for large values of | (b) Find the x- and y-intercepts of the graph.
(c) Determine whether the graph crosses or touches the x-axis at each x-intercept.
(d) Graph f using a graphing utility.
(e) Use the graph to determine the local maxima and local minima, if any exist. Round turning points to two decimal places.
(f) Use the information obtained in (a) - (e) to draw a complete graph of f by hand. Label all intercepts and turning points.
(g) Find the domain of f. Use the graph to find the range of f.
(h) Use the graph to determine where f is increasing and where f is decreasing.
-
(Essay)
5.0/5  (47)
(47)
Use the graph to find the oblique asymptote, if any, of the function.
-
(Multiple Choice)
4.9/5  (38)
(38)
Use Descartes' Rule of Signs and the Rational Zeros Theorem to find all the real zeros of the polynomial function. Use the
zeros to factor f over the real numbers.
-
(Multiple Choice)
4.9/5  (36)
(36)
Solve the problem.
-A lens can be used to create an image of an object on the opposite side of the lens, such as the image created on a
movie screen. Every lens has a measurement called its focal length, f. The distance s1 of the object to the lens is
related to the distance of the lens to the image by the function For a lens with f = 0.3 m, what are the asymptotes of this function?
(Essay)
4.7/5  (30)
(30)
Solve the problem.
-For what positive numbers will the cube of a number exceed 9 times its square? A)
B)
C)
D)
(Multiple Choice)
4.7/5  (43)
(43)
Use the graph to find the vertical asymptotes, if any, of the function.
-
(Multiple Choice)
4.8/5  (35)
(35)
For the polynomial, list each real zero and its multiplicity. Determine whether the graph crosses or touches the x-axis at
each x -intercept.
-
(Multiple Choice)
4.9/5  (44)
(44)
Showing 41 - 60 of 350
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)