Exam 3: Statistics for Describing, Exploring, and Comparing Data
Exam 1: Introduction to Statistics85 Questions
Exam 2: Summarizing and Graphing Data82 Questions
Exam 3: Statistics for Describing, Exploring, and Comparing Data149 Questions
Exam 4: Probability170 Questions
Exam 5: Probability Distributions158 Questions
Exam 6: Normal Probability Distributions173 Questions
Exam 7: Estimates and Sample Sizes139 Questions
Exam 8: Hypothesis Testing130 Questions
Exam 9: Inferences From Two Samples105 Questions
Exam 10: Correlation and Regression129 Questions
Exam 11: Multinomial Experiments and Contingency Tables31 Questions
Exam 12: Analysis of Variance60 Questions
Exam 13: Nonparametric Statistics64 Questions
Exam 14: Statistical Process Control38 Questions
Select questions type
Find the variance for the given data. Round your answer to one more decimal place than the original data.
-The normal monthly precipitation (in inches)for August is listed for 12 different U.S. cities.
3.5 1.6 2.4 3.7 4.1 3.9
1.0 3.6 4.2 3.4 3.7 2.2
Compute the variance.
(Multiple Choice)
4.8/5  (41)
(41)
Find the mean of the data summarized in the given frequency distribution.
-The test scores of 40 students are summarized in the frequency distribution below. Find the mean score. Score Students 50-59 7 60-69 5 70-79 10 80-89 6 90-99 12
(Multiple Choice)
4.7/5  (38)
(38)
Find the percentile for the data point.
-The test scores of 40 students are listed below. Find P85. 30 35 43 44 47 48 54 55 56 57 59 62 63 65 66 68 69 69 71 72 72 73 74 76 77 77 78 79 80 81 81 82 83 85 89 92 93 94 97 98
(Multiple Choice)
5.0/5  (30)
(30)
Find the variance for the given data. Round your answer to one more decimal place than the original data.
-Christine is currently taking college astronomy. The instructor often gives quizzes. On the past seven quizzes, Christine got the following scores: 50 12 38 25 16 48 58 Compute the standard deviation s.
(Multiple Choice)
4.8/5  (25)
(25)
Answer the question.
-A store manager kept track of the number of newspapers sold each week over a seven-week period. The results are shown below. 78, 43, 228, 194, 259, 236, 235 Find the median number of newspapers sold.
(Multiple Choice)
4.8/5  (37)
(37)
Find the median for the given sample data.
-20, 21, 46, 21, 49, 21, 49
(Multiple Choice)
4.9/5  (34)
(34)
Human body temperatures have a mean of 98.20° F and a standard deviation of 0.62°. Sally's temperature can be described by z = 2.1. What is her temperature? Round your answer to the nearest hundredth.
(Multiple Choice)
4.7/5  (32)
(32)
Find the z-score corresponding to the given value and use the z-score to determine whether the value is unusual.
Consider a score to be unusual if its z-score is less than -2.00 or greater than 2.00. Round the z-score to the nearest tenth
if necessary.
-Which is better: a score of 82 on a test with a mean of 70 and a standard deviation of 8, or a score of 82 on a test with a mean of 75 and a standard deviation of 4?
(Multiple Choice)
4.8/5  (26)
(26)
Solve the problem.
-Skewness can be measured by Pearson's index of skewness: If or , the data can be considered significantly skewed. Would you expect that incomes of all adults in the US would be skewed? In which direction? Why? Would you expect that for these incomes, Pearson's index of skewness would be greater than 1 , smaller than , or between and 1 ?
(Essay)
4.8/5  (26)
(26)
Solve the problem.
-The harmonic mean is often used as a measure of center for data sets consisting of rates of change, such as speeds. It is found by dividing the number of values (n)by the sum of the reciprocals of all values, expressed as Pierre drives to work (a distance of 57 miles)at a speed of 73 mi/h and returns home at a speed of 53 mi/h. What is his average speed for the round trip? Use the harmonic mean.
(Multiple Choice)
4.8/5  (37)
(37)
Solve the problem.
-In chemistry, the Kelvin scale is often used to measure temperatures. On the Kelvin scale, zero degrees is absolute zero. Temperatures on the Kelvin scale are related to temperatures on the Celsius scale as follows: K = C + 273°. Temperatures on the Fahrenheit scale are related to temperatures on the Celsius scale as follows: A set of temperatures is given in Celsius, Kelvin, and Fahrenheit. How will the standard deviations of the three sets of data compare?
(Essay)
4.8/5  (37)
(37)
Find the standard deviation of the data summarized in the given frequency distribution.
-A body temperature of 96.8° F given that human body temperatures have a mean of 98.20° F and a standard deviation of 0.62°.
(Multiple Choice)
4.8/5  (37)
(37)
Find the mean, median, mode, and midrange for each of the two samples, then compare the two sets of results.
-The Body Mass Index (BMI)is measured for a random sample of men and women. Interpret the results by determining whether there is a difference between the two data sets that is not apparent from a comparison of the measures of center. If there is, what is it? Men 24 23.5 20 27 29 22.5 28 24 Women 18 20 24 25 27 21 22 25
(Essay)
4.8/5  (48)
(48)
Provide an appropriate response.
-The weekly salaries (in dollars)of 24 randomly selected employees of a company are shown below. Construct a boxplot for the data set. 310 320 450 460 470 500 520 540 580 600 650 700 710 840 870 900 1000 1200 1250 1300 1400 1720 2500 3700
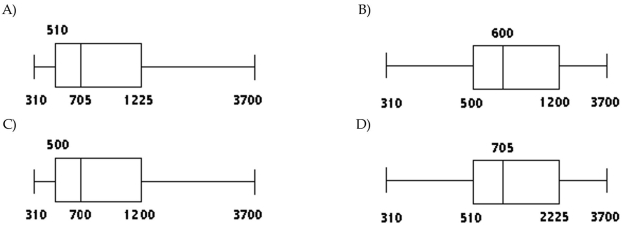
(Short Answer)
4.9/5  (33)
(33)
Find the mean for the given sample data.
-Frank's Furniture employees earned the following amounts last week: \ 453.83 \ 529.91 \ 439.27 \ 309.23 \ 453.86 \ 533.25 \ 457.25 \ 156.42 \ 152.64 What was the mean amount earned by an employee last week? Round your answer to the nearest cent.
(Multiple Choice)
4.9/5  (39)
(39)
Provide an appropriate response.
-When finding percentiles, if the locator L is not a whole number, one procedure is to interpolate so that a locator of 23.75, for example, leads to a value that is 3/4 of the way between the 23rd and 24th scores. Use this method of interpolation to find P75 for the set of test scores below. 51 54 64 68 72 74
76 83 86 94 99
(Multiple Choice)
4.8/5  (38)
(38)
Solve the problem. Round results to the nearest hundredth.
-The mean of a set of data is 4.68 and its standard deviation is 2.83. Find the z score for a value of 9.38.
(Multiple Choice)
4.8/5  (32)
(32)
Solve the problem.
-The heights in feet of people who work in an office are as follows. Use the range rule of thumb to find the standard deviation. Round results to the nearest tenth. 5.9 6.0 5.8 5.4 6.0 5.5 6.0 6.2 6.1 5.5
(Multiple Choice)
4.9/5  (36)
(36)
Find the mean for the given sample data.
-The local Tupperware dealers earned these commissions last month:
What was the mean commission earned? Round your answer to the nearest cent.
(Multiple Choice)
4.9/5  (33)
(33)
Solve the problem.
-The geometric mean is often used in business and economics for finding average rates of change, average rates of growth, or average ratios. Given n values (all positive), the geometric mean is the nth root of their product. The average growth factor for money compounded at annual interest rates of 49%, 19%, 24%, and 13% can be found by computing the geometric mean of 1.49, 1.19, 1.24, and 1.13. Find that average growth factor.
(Multiple Choice)
4.9/5  (37)
(37)
Showing 121 - 140 of 149
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)