Exam 4: Graphs of the Circular Functions
Exam 1: Trigonometric Functions188 Questions
Exam 2: Acute Angles and Right Triangles204 Questions
Exam 3: Radian Measure and the Unit Circle167 Questions
Exam 4: Graphs of the Circular Functions137 Questions
Exam 5: Trigonometric Identities321 Questions
Exam 6: Inverse Circular Functions and Trigonometric Equations179 Questions
Exam 7: Applications of Trigonometry and Vectors103 Questions
Exam 8: Complex Numbers, Polar Equations, and Parametric Equations60 Questions
Select questions type
Solve the problem.
-A weight attached to a spring is pulled down 5 inches below the equilibrium position. Assuming that the period of the system is , what is the frequency of the system?
(Multiple Choice)
4.8/5  (47)
(47)
Use Identities to find the exact value.
-A weight attached to a spring is pulled down 4 inches below the equilibrium position. Assuming that the frequency of the system is cycles per second, determine a trigonometric model that gives the position of the weight at time seconds.
(Multiple Choice)
4.9/5  (27)
(27)
Match the function with its graph.
-1)
2)
3)
4)
a)
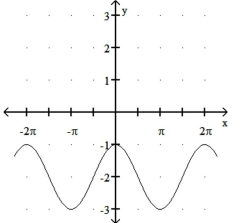 b)
b)
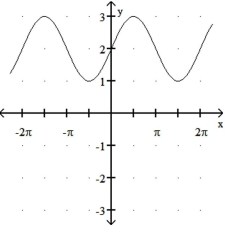 c)
c)
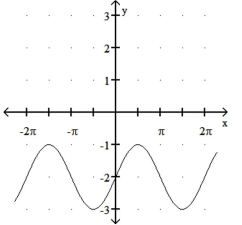 d)
d)
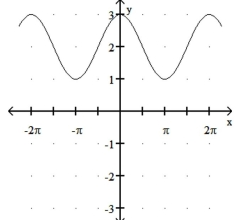
(Multiple Choice)
4.9/5  (36)
(36)
Match the function with its graph.
-1)
2)
3)
4)
a)
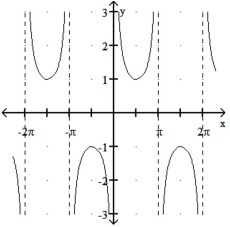 b)
b)
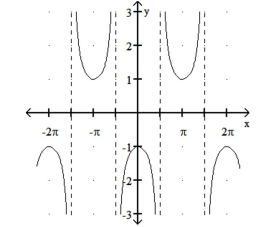 c)
c)
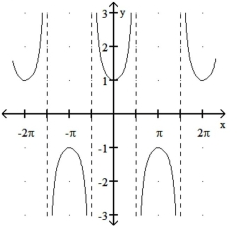 d)
d)
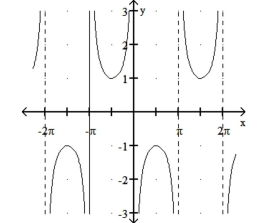
(Multiple Choice)
4.8/5  (31)
(31)
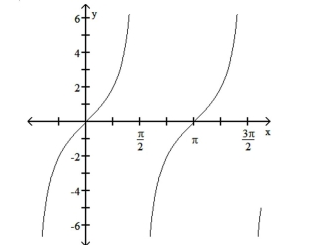
The function graphed is of the form y = a tan bx or y = a cot bx, where b > 0. Determine the equation of the graph.
-
(Multiple Choice)
4.9/5  (38)
(38)
Solve the problem.
-Ignoring friction, the time, (in seconds), required for a block to slide down an inclined plane is given by the formula where is the length of the base in feet and feet per second is the acceleration of gravity. How long does it take a block to slide down an inclined plane with a base of 12 feet at an angle of ? Round your answer to three decimal places.
(Multiple Choice)
4.9/5  (35)
(35)
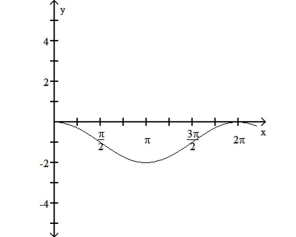
The function graphed is of the form y = cos x + c, y = sin x + c, y = cos(x - d), or y = sin(x - d), where d is the least possible
positive value. Determine the equation of the graph.
-
(Multiple Choice)
4.7/5  (44)
(44)
Solve the problem.
-A generator produces an alternating current according to the equation I = 48 sin 109πt, where t is time in seconds and I is the current in amperes. What is the smallest time t such that I = 24?
(Multiple Choice)
4.9/5  (38)
(38)
Solve the problem.
-Determine the length of a pendulum that has a period of 4 seconds.
(Multiple Choice)
4.7/5  (37)
(37)
Showing 81 - 100 of 137
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)