Exam 4: Graphs of the Circular Functions
Exam 1: Trigonometric Functions188 Questions
Exam 2: Acute Angles and Right Triangles204 Questions
Exam 3: Radian Measure and the Unit Circle167 Questions
Exam 4: Graphs of the Circular Functions137 Questions
Exam 5: Trigonometric Identities321 Questions
Exam 6: Inverse Circular Functions and Trigonometric Equations179 Questions
Exam 7: Applications of Trigonometry and Vectors103 Questions
Exam 8: Complex Numbers, Polar Equations, and Parametric Equations60 Questions
Select questions type
Solve the problem.
-The chart represents the amount of fuel consumed by a machine used in manufacturing. The machine is turned on at the beginning of the day, takes a certain amount of time to reach its full
Power (the point at which it uses the most fuel per hour), runs for a certain number of hours, and is
Shut off at the end of the work day. The fuel usage per hour of the machine is represented by a
Periodic function. What is the period in hours of this function? 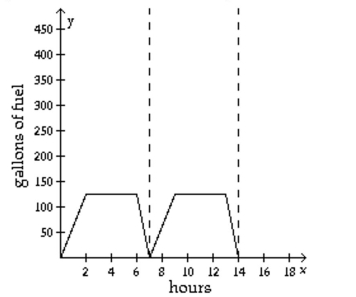
(Multiple Choice)
4.8/5  (37)
(37)
The function graphed is of the form y = a sin bx or y = a cos bx, where b > 0. Determine the equation of the graph. 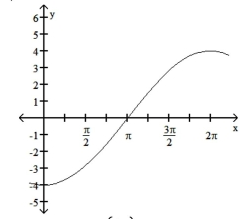 A)
B)
C)
D)
-The function graphed is of the form y = a sin bx or y = a cos bx, where b > 0. Determine the equation of the graph.
A)
B)
C)
D)
-The function graphed is of the form y = a sin bx or y = a cos bx, where b > 0. Determine the equation of the graph. 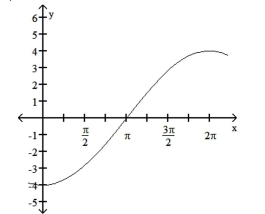
(Multiple Choice)
4.9/5  (29)
(29)
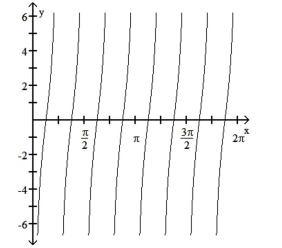
The function graphed is of the form y = a tan bx or y = a cot bx, where b > 0. Determine the equation of the graph.
-
(Multiple Choice)
4.9/5  (27)
(27)
Solve the problem.
-The position of a weight attached to a spring is inches after seconds. When does the weight first reach its maximum height?
(Multiple Choice)
5.0/5  (36)
(36)
Solve the problem.
-The position of a weight attached to a spring is inches after seconds. What are the frequency and period of the system?
(Multiple Choice)
4.8/5  (33)
(33)
The function graphed is of the form y = a sin bx or y = a cos bx, where b > 0. Determine the equation of the graph.
-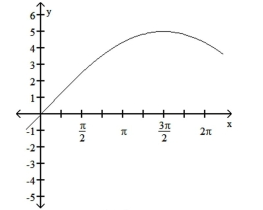
(Multiple Choice)
4.8/5  (39)
(39)
Solve the problem.
-The total sales in dollars of some small businesses fluctuates according to the equation , where is the time in months, with corresponding to January, , and . Determine the month with the greatest total sales and give the sales in that month.
(Multiple Choice)
4.7/5  (36)
(36)
Solve the problem.
-A pendulum of length , when displaced horizontally and released, oscillates with harmonic motion according to the equation , where is the distance in meters from the rest position seconds after release, and . Identify the period, amplitude, and phase shift when and . Round all answers to the nearest hundredth.
(Multiple Choice)
4.9/5  (37)
(37)
Match the function with its graph.
-1)
2)
3)
4)
a)
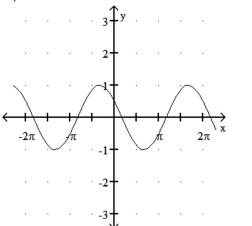 b)
b)
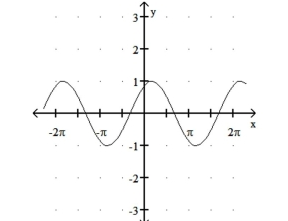 c)
c)
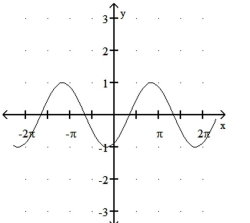 d)
d)
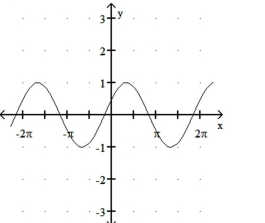
(Multiple Choice)
5.0/5  (35)
(35)
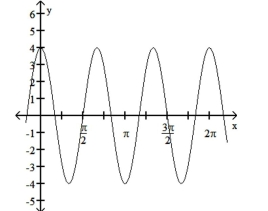
The function graphed is of the form y = a sin bx or y = a cos bx, where b > 0. Determine the equation of the graph.
-
(Multiple Choice)
4.9/5  (39)
(39)
Solve the problem.
-The minimum length of a highway sag curve can be computed by
where is the downhill grade in degrees is the uphill grade in degrees , is the safe stopping distance for a given speed limit, is the height of the headlights, and is the alignment of the headlights in degrees. Compute for a 55-mph speed limit, where , , and . Round your answer to the nearest foot.
(Multiple Choice)
4.9/5  (31)
(31)
Match the function with its graph.
29
-1) 2)
3) 4)
a)
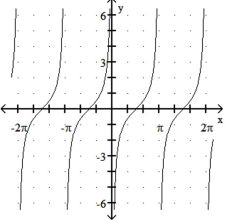 b)
b)
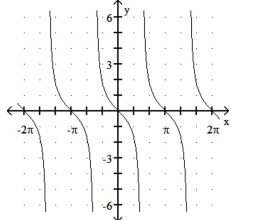 c)
c)
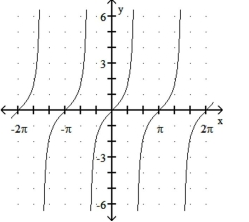 d)
d)
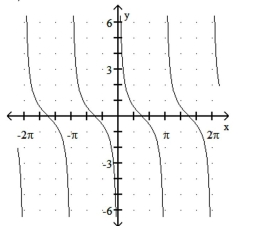
(Multiple Choice)
4.7/5  (27)
(27)
Solve the problem.
-The voltage in an electrical circuit is given by , where is time measured in seconds. Find the frequency of the function (that is, find the number of cycles or periods completed in one second).
(Multiple Choice)
4.9/5  (37)
(37)
Showing 21 - 40 of 137
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)