Exam 4: Graphs of the Circular Functions
Exam 1: Trigonometric Functions188 Questions
Exam 2: Acute Angles and Right Triangles204 Questions
Exam 3: Radian Measure and the Unit Circle167 Questions
Exam 4: Graphs of the Circular Functions137 Questions
Exam 5: Trigonometric Identities321 Questions
Exam 6: Inverse Circular Functions and Trigonometric Equations179 Questions
Exam 7: Applications of Trigonometry and Vectors103 Questions
Exam 8: Complex Numbers, Polar Equations, and Parametric Equations60 Questions
Select questions type
Solve the problem.
-For an electrical circuit, the voltage is modeled by , where is the time in seconds. How many cycles are completed in one second?
(Multiple Choice)
4.8/5  (26)
(26)
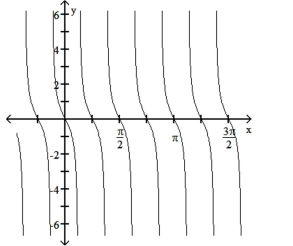
The function graphed is of the form y = a tan bx or y = a cot bx, where b > 0. Determine the equation of the graph.
-
(Multiple Choice)
4.8/5  (34)
(34)
Solve the problem.
-The chart represents the amount of fuel consumed by a machine used in manufacturing. The machine is turned on at the beginning of the day, takes a certain amount of time to reach its full
Power (the point at which it uses the most fuel per hour), runs for a certain number of hours, and is
Shut off at the end of the work day. The fuel usage per hour of the machine is represented by a
Periodic function. When does the machine first reach its full power? 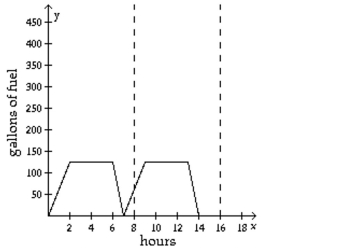
(Multiple Choice)
4.8/5  (42)
(42)
Determine the equation of the graph. 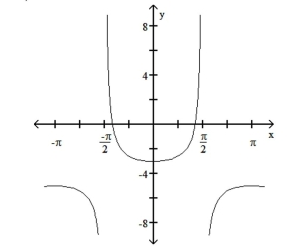 A)
B)
C)
D)
-Determine the equation of the graph.
A)
B)
C)
D)
-Determine the equation of the graph. 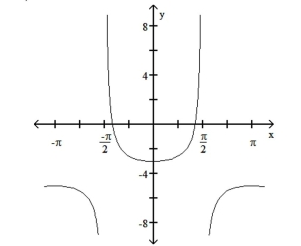
(Multiple Choice)
4.9/5  (37)
(37)
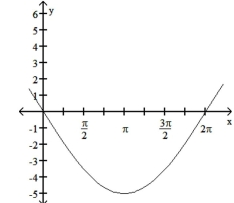
The function graphed is of the form y = a sin bx or y = a cos bx, where b > 0. Determine the equation of the graph.
-
(Multiple Choice)
4.8/5  (35)
(35)
Solve the problem.
-A guitar string is plucked so that it vibrates with a frequency of F = 66. Suppose the maximum displacement at the center of the string is s(0)= 0.58. Find an equation of the form s(t)= a cos bt to
Model this displacement. Round constants to 2 decimal places.
(Multiple Choice)
4.7/5  (31)
(31)
Solve the problem.
-Use regression to find constants a, b, c, and d so that f(x)= a sin (bx + c)+ d models the data given below. Round all answers to 9 decimal places. Month 1 2 3 4 5 6 7 8 9 10 11 12 Precipitation (inches) 1 3 6 9 11 12 11 9 7 5 3 2
(Multiple Choice)
5.0/5  (31)
(31)
Match the function with its graph.
-1) y = sin 3x
2) y = 3 cos x
3) y = 3 sin x
4) y = cos 3x
a)
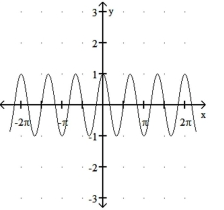 b)
b)
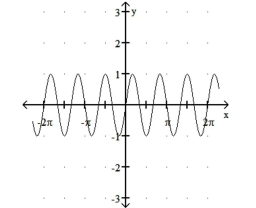 c)
c)
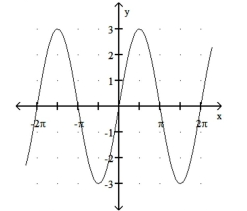 d)
d)
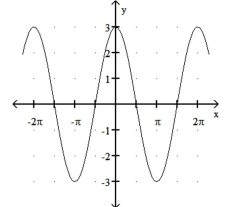
(Multiple Choice)
4.9/5  (34)
(34)
Solve the problem.
-The path of a projectile fired at an inclination to the horizontal with an initial speed is a parabola. The range of the projectile, the horizontal distance that the projectile travels, is found by the formula where feet per second per second or meters per second per second. Find the range of a projectile fired with an initial velocity of 140 feet per second at an angle of to the horizontal. Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (44)
(44)
Solve the problem.
-A coil of wire rotating in a magnetic field induces a voltage given by
where is time in seconds. Find the smallest positive time to produce a voltage of .
(Multiple Choice)
4.7/5  (42)
(42)
Showing 101 - 120 of 137
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)