Exam 10: Two-Sample Tests

TABLE 10-6 To investigate the efficacy of a diet, a random sample of 16 male patients is selected from a population of adult males using the diet. The weight of each individual in the sample is taken at the start of the diet and at a medical follow-up 4 weeks later. Assuming that the population of differences in weight before versus after the diet follow a normal distribution, the t test for related samples can be used to determine if there was a significant decrease in the mean weight during this period. Suppose the mean decrease in weights over all 16 subjects in the study is 3.0 pounds with the standard deviation of differences computed as 6.0 pounds. -Referring to Table 10-6, a one-tail test of the null hypothesis of no difference would ________ (be rejected/not be rejected) at the α = 0.05 level of significance.

TABLE 10-4 Two samples each of size 25 are taken from independent populations assumed to be normally distributed with equal variances. The first sample has a mean of 35.5 and standard deviation of 3.0 while the second sample has a mean of 33.0 and standard deviation of 4.0. -Referring to Table 10-4, a two-tail test of the null hypothesis of no difference would ________ (be rejected/not be rejected) at the α = 0.05 level of significance.

TABLE 10-14 The use of preservatives by food processors has become a controversial issue. Suppose two preservatives are extensively tested and determined safe for use in meats. A processor wants to compare the preservatives for their effects on retarding spoilage. Suppose 15 cuts of fresh meat are treated with preservative I and 15 are treated with preservative II, and the number of hours until spoilage begins is recorded for each of the 30 cuts of meat. The results are summarized in the table below. Preservative I Preservative II I 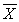= 106.4 hours 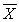II = 96.54 hours SI = 10.3 hours SII = 13.4 hours -Referring to Table 10-14, what assumptions are necessary for testing if the population variances differ for preservatives I and II?

TABLE 10-13 The amount of time required to reach a customer service representative has a huge impact on customer satisfaction. Below is the Excel output from a study to see whether there is evidence of a difference in the mean amounts of time required to reach a customer service representative between two hotels. Assume that the population variances in the amount of time for the two hotels are not equal. 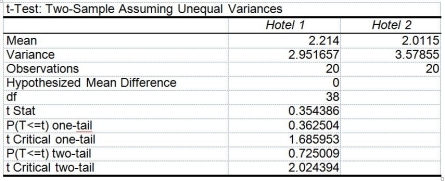-Referring to Table 10-13, what is the value of the test statistic?

The Wall Street Journal recently ran an article indicating differences in perception of sexual harassment on the job between men and women. The article claimed that women perceived the problem to be much more prevalent than did men. One question asked to both men and women was: "Do you think sexual harassment is a major problem in the American workplace?" Some 24% of the men compared to 62% of the women responded "Yes." Suppose that 150 women and 200 men were interviewed. Construct a 90% confidence interval estimate of the difference between the proportion of women and men who think sexual harassment is a major problem in the American workplace.

In testing for the differences between the means of 2 independent populations where the variances in each population are unknown but assumed equal, the degrees of freedom are

TABLE 10-13 The amount of time required to reach a customer service representative has a huge impact on customer satisfaction. Below is the Excel output from a study to see whether there is evidence of a difference in the mean amounts of time required to reach a customer service representative between two hotels. Assume that the population variances in the amount of time for the two hotels are not equal. -Referring to Table 10-13, what is the smallest level of significance at which the null hypothesis will still not be rejected?

TABLE 10-15 The table below presents the summary statistics for the starting annual salaries (in thousands of dollars) for individuals entering the public accounting and financial planning professions. Sample I (public accounting): 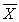₁ = 60.35, S₁ = 3.25, n₁ = 12 Sample II (financial planning): 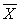₂ = 58.20, S₂ = 2.48, n₂ = 14 Test whether the mean starting annual salaries for individuals entering the public accounting professions is higher than that of financial planning assuming that the two population variances are the same. -Referring to Table 10-15, suppose α = 0.05. Which of the following represents the result of the test on a difference in the variances?

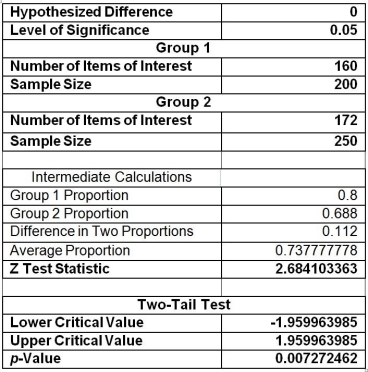
TABLE 10-3 A real estate company is interested in testing whether the mean time that families in Gotham have been living in their current homes is less than families in Metropolis. Assume that the two population variances are equal. A random sample of 100 families from Gotham and a random sample of 150 families in Metropolis yield the following data on length of residence in current homes. Gotham: 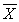G = 35 months, SG² = 900 Metropolis: 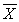M = 50 months, SM² = 1050 -Referring to Table 10-3, what is the estimated standard error of the difference between the 2 sample means?

TABLE 10-4 Two samples each of size 25 are taken from independent populations assumed to be normally distributed with equal variances. The first sample has a mean of 35.5 and standard deviation of 3.0 while the second sample has a mean of 33.0 and standard deviation of 4.0. -Referring to Table 10-4, there are ________ degrees of freedom for this test.

TABLE 10-4 Two samples each of size 25 are taken from independent populations assumed to be normally distributed with equal variances. The first sample has a mean of 35.5 and standard deviation of 3.0 while the second sample has a mean of 33.0 and standard deviation of 4.0. -Referring to Table 10-4, if you were interested in testing against the one-tail alternative that μ₁ > μ₂ at the α = 0.01 level of significance, the null hypothesis would ________ (be rejected/not be rejected).

When you test for differences between the means of two independent populations, you can only use a two-tail test.

TABLE 10-8 A few years ago, Pepsi invited consumers to take the "Pepsi Challenge." Consumers were asked to decide which of two sodas, Coke or Pepsi, they preferred in a blind taste test. Pepsi was interested in determining what factors played a role in people's taste preferences. One of the factors studied was the gender of the consumer. Below are the results of analyses comparing the taste preferences of men and women with the proportions depicting preference for Pepsi. Males: n = 109, pM = 0.422018 Females: n = 52, pF = 0.25 pM - pF = 0.172018 Z = 2.11825 -Referring to Table 10-8, construct a 95% confidence interval estimate of the difference between the proportion of males and females who prefer Pepsi.

TABLE 10-10 A corporation randomly selects 150 salespeople and finds that 66% who have never taken a self-improvement course would like such a course. The firm did a similar study 10 years ago in which 60% of a random sample of 160 salespeople wanted a self-improvement course. The groups are assumed to be independent random samples. Let π₁ and π₂ represent the true proportion of workers who would like to attend a self-improvement course in the recent study and the past study, respectively. -Referring to Table 10-10, what is/are the critical value(s) when testing whether the current population proportion is higher than before if α = 0.05?

TABLE 10-9 The following Excel output contains the results of a test to determine whether the proportions of satisfied customers at two resorts are the same or different. -Referring to Table 10-9, construct a 95% confidence interval estimate of the difference in the population proportion of satisfied guests between the two resorts.

TABLE 10-6 To investigate the efficacy of a diet, a random sample of 16 male patients is selected from a population of adult males using the diet. The weight of each individual in the sample is taken at the start of the diet and at a medical follow-up 4 weeks later. Assuming that the population of differences in weight before versus after the diet follow a normal distribution, the t test for related samples can be used to determine if there was a significant decrease in the mean weight during this period. Suppose the mean decrease in weights over all 16 subjects in the study is 3.0 pounds with the standard deviation of differences computed as 6.0 pounds. -Referring to Table 10-6, what is the 99% confidence interval estimate for the mean difference in weight before and after the diet?

In testing for differences between the means of 2 related populations where the variance of the differences is unknown, the degrees of freedom are

If we are testing for the difference between the means of 2 independent populations presuming equal variances with samples of n₁ = 20 and n₂ = 20, the number of degrees of freedom is equal to

TABLE 10-7 A buyer for a manufacturing plant suspects that his primary supplier of raw materials is overcharging. In order to determine if his suspicion is correct, he contacts a second supplier and asks for the prices on various identical materials. He wants to compare these prices with those of his primary supplier. The data collected is presented in the table below, with some summary statistics presented (all of these might not be necessary to answer the questions which follow). The buyer believes that the differences are normally distributed and will use this sample to perform an appropriate test at a level of significance of 0.01. Primary Secondary Material Supplier Supplier Difference 1 $55 $45 $10 2 $48 $47 $1 3 $31 $32 -$1 4 $83 $77 $6 5 $37 $37 $0 6 $55 $54 $1 Sum: $309 $292 $17 Sum of Squares: $17,573 $15,472 $139 -Referring to Table 10-7, the test to perform is a

TABLE 10-8 A few years ago, Pepsi invited consumers to take the "Pepsi Challenge." Consumers were asked to decide which of two sodas, Coke or Pepsi, they preferred in a blind taste test. Pepsi was interested in determining what factors played a role in people's taste preferences. One of the factors studied was the gender of the consumer. Below are the results of analyses comparing the taste preferences of men and women with the proportions depicting preference for Pepsi. Males: n = 109, pM = 0.422018 Females: n = 52, pF = 0.25 pM - pF = 0.172018 Z = 2.11825 -Referring to Table 10-8, construct a 99% confidence interval estimate of the difference between the proportion of males and females who prefer Pepsi.