Exam 7: Systems and Matrices
Exam 1: Functions and Graphs362 Questions
Exam 2: Polynomial, Power, and Rational Functions494 Questions
Exam 3: Exponential, Logistic, and Logarithmic Functions350 Questions
Exam 4: Trigonometric Functions522 Questions
Exam 5: Analytic Trigonometry313 Questions
Exam 6: Applications of Trigonometry333 Questions
Exam 7: Systems and Matrices354 Questions
Exam 8: Analytic Geometry in Two and Three Dimensions167 Questions
Exam 9: Discrete Mathematics154 Questions
Exam 10: Statistics and Probability147 Questions
Exam 11: An Introduction to Calculus: Limits, Derivatives, and Integrals167 Questions
Exam 12: Prerequisites382 Questions
Select questions type
Determine which elementary row operation(s) applied to the first matrix will yield the second matrix.
-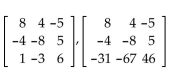
(Essay)
4.7/5  (37)
(37)
Suppose that you are solving a system of 4 linear equations in 4 variables by the row echelon method. If you use the transformation , which row or rows of the augmented matrix, if any, will change?
(Multiple Choice)
4.9/5  (34)
(34)
Solve the system of equations by finding the reduced row echelon form for the augmented matrix.
- x+y+z=1 x-y+4z=16 2x+y+z=2
(Multiple Choice)
4.9/5  (48)
(48)
Solve the problem.
-The sum of three numbers is 2 . The first, minus the second, plus 4 times the third, is 21 . The third, plus 5 times the first, plus the second, is . What are the numbers?
(Multiple Choice)
4.9/5  (38)
(38)
Solve the problem.
-An airline with two types of airplanes, and , has contracted with a tour group to provide transportation for a minimum of 400 first class, 900 tourist class, and 1500 economy class passengers. For a certain trip, airplane costs to operate and can accommodate 20 first class, 50 tourist class, and 110 economy class passengers. Airplane costs to operate and can accommodate 18 first class, 30 tourist class, and 44 economy class passengers. How many of each type of airplane should be used in order to minimize the operating cost?
(Multiple Choice)
4.9/5  (34)
(34)
Find the indicated matrix product or state that the product is undefined.
-
(Multiple Choice)
4.7/5  (42)
(42)
Find a matrix A and a column matrix B that describe the following tables involving credits and tuition costs. Find the
matrix product AB, and interpret the significance of the entries of this product.
-
(Multiple Choice)
4.8/5  (31)
(31)
Suppose that you are solving a system of three linear equations in three variables by the row echelon method ans obtain the following augmented matrix.
What row transformation would you perform next?
(Multiple Choice)
4.9/5  (39)
(39)
Showing 21 - 40 of 354
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)