Exam 7: Systems and Matrices
Exam 1: Functions and Graphs362 Questions
Exam 2: Polynomial, Power, and Rational Functions494 Questions
Exam 3: Exponential, Logistic, and Logarithmic Functions350 Questions
Exam 4: Trigonometric Functions522 Questions
Exam 5: Analytic Trigonometry313 Questions
Exam 6: Applications of Trigonometry333 Questions
Exam 7: Systems and Matrices354 Questions
Exam 8: Analytic Geometry in Two and Three Dimensions167 Questions
Exam 9: Discrete Mathematics154 Questions
Exam 10: Statistics and Probability147 Questions
Exam 11: An Introduction to Calculus: Limits, Derivatives, and Integrals167 Questions
Exam 12: Prerequisites382 Questions
Select questions type
Determine which elementary row operation(s) applied to the first matrix will yield the second matrix.
-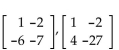
(Essay)
4.9/5  (44)
(44)
Solve the system of equations by finding the reduced row echelon form for the augmented matrix.
- x+4y+5z=-27 4y+4z=-24 z=-4
(Multiple Choice)
4.9/5  (36)
(36)
Use a graph to determine the number of solutions the system has.
- 6x-9y=3 -10x+15y=5
(Multiple Choice)
4.9/5  (32)
(32)
Solve the system of equations by using an inverse matrix.
- 5x+4y=8 4x-2y=22
(Multiple Choice)
4.8/5  (51)
(51)
Graph the system of inequalities. Shade the region that represents the solution set.
- + \leq16 x+y <1
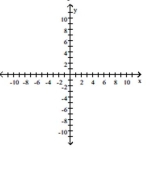
(Multiple Choice)
4.7/5  (36)
(36)
Decide whether the ordered pair is a solution of the given system.
- (1,3) y=+5x-3 y=6x-3
(True/False)
4.8/5  (28)
(28)
Fill in the blanks to complete the statement. For a system of 6 equations and 6 unknowns, the corresponding augmented matrix will have rows and ? columns.
(Multiple Choice)
5.0/5  (38)
(38)
Solve the system of inequalities.
- 2x+3y\leq6 x-y\geq3 x\geq1
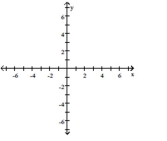
(Multiple Choice)
4.9/5  (45)
(45)
Solve the system of equations by using an inverse matrix.
-4x + y - 2z - w = 6 -x + 4y + z - 2w = 10
4x - 2y + 4z + w = -22
-2x - y - z - 2w = 7
(Multiple Choice)
4.8/5  (34)
(34)
Decide whether the ordered pair is a solution of the given system.
- (-1,4) y=+5 2x+y=4
(True/False)
4.9/5  (47)
(47)
Find the inverse of A if it has one, or state that the inverse does not exist.
-
(Multiple Choice)
4.7/5  (45)
(45)
Solve the problem.
-Find the equilibrium point for the given demand and supply curve. p = 4830 - 90x (demand)
P = 120x (supply)
(Multiple Choice)
4.9/5  (44)
(44)
Solve the problem.
-Find the minimum value of subject to the following constraints.
2x-4y\leq10 2x+y\geq15 x\geq0 y\geq0
(Multiple Choice)
4.8/5  (37)
(37)
Showing 61 - 80 of 354
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)