Exam 2: Polynomial, Power, and Rational Functions
Exam 1: Functions and Graphs362 Questions
Exam 2: Polynomial, Power, and Rational Functions494 Questions
Exam 3: Exponential, Logistic, and Logarithmic Functions350 Questions
Exam 4: Trigonometric Functions522 Questions
Exam 5: Analytic Trigonometry313 Questions
Exam 6: Applications of Trigonometry333 Questions
Exam 7: Systems and Matrices354 Questions
Exam 8: Analytic Geometry in Two and Three Dimensions167 Questions
Exam 9: Discrete Mathematics154 Questions
Exam 10: Statistics and Probability147 Questions
Exam 11: An Introduction to Calculus: Limits, Derivatives, and Integrals167 Questions
Exam 12: Prerequisites382 Questions
Select questions type
Solve the problem.
- gives the alcohol level in an average person's blood hrs after drinking 8 oz of 100 -proof whiskey. If the level exceeds units, a person is legally drunk. Would a person be drunk after 5 hours?
(Multiple Choice)
4.9/5  (33)
(33)
State the power and constant of variation for the function, and then analyze it.
-
(Essay)
4.8/5  (32)
(32)
Write the statement as a power function equation. Use k as the constant of variation.
-The height h of a cone with a fixed volume varies inversely as the square of its radius r.
(Multiple Choice)
4.9/5  (41)
(41)
Solve the problem.
-The profit made when units are sold, , is given by . Determine the number of units to be sold in order for (a loss is taken).
(Multiple Choice)
4.9/5  (35)
(35)
Use the Rational Zeros Theorem to write a list of all potential rational zeros
-
(Multiple Choice)
4.9/5  (35)
(35)
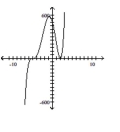
Match the polynomial function graph to the appropriate zeros and multiplicities.
-
(Multiple Choice)
4.8/5  (36)
(36)
Solve the problem.
-The profit made when units are sold, , is given by . Determine the number of units to be sold in order for (a profit is made).
(Multiple Choice)
4.9/5  (40)
(40)
Find the requested function.
-Find the polynomial function with leading coefficient ; degree 3 ; and , and 5 as zeros.
(Multiple Choice)
4.9/5  (37)
(37)
Find all of the real zeros of the function. Give exact values whenever possible. Identify each zero as rational or irrational.
-
(Multiple Choice)
4.7/5  (33)
(33)
Determine if the function is a monomial function (given that c and k represent constants). If it is, state the degree and
leading coefficient.
-
(Multiple Choice)
4.8/5  (37)
(37)
Write the function as a product of linear and irreducible quadratic factors, all with real coefficients.
-
(Multiple Choice)
4.9/5  (38)
(38)
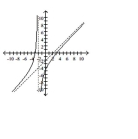
Match the graph of the rational function with its equation.
-
(Multiple Choice)
4.7/5  (40)
(40)
Describe the end behavior of the polynomial function by finding 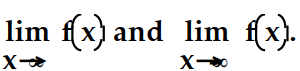 -
-
(Multiple Choice)
4.8/5  (32)
(32)
Solve the problem.
-A coin is tossed upward with an initial velocity of . During what interval of time will the coin be at a height of at least ? .
(Multiple Choice)
4.7/5  (42)
(42)
Showing 261 - 280 of 494
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)