Exam 2: Polynomial, Power, and Rational Functions
Exam 1: Functions and Graphs362 Questions
Exam 2: Polynomial, Power, and Rational Functions494 Questions
Exam 3: Exponential, Logistic, and Logarithmic Functions350 Questions
Exam 4: Trigonometric Functions522 Questions
Exam 5: Analytic Trigonometry313 Questions
Exam 6: Applications of Trigonometry333 Questions
Exam 7: Systems and Matrices354 Questions
Exam 8: Analytic Geometry in Two and Three Dimensions167 Questions
Exam 9: Discrete Mathematics154 Questions
Exam 10: Statistics and Probability147 Questions
Exam 11: An Introduction to Calculus: Limits, Derivatives, and Integrals167 Questions
Exam 12: Prerequisites382 Questions
Select questions type
Determine the x values that cause the function to be (a) zero, (b) undefined, (c) positive, and (d) negative.
-
(Multiple Choice)
4.9/5  (46)
(46)
Determine the x values that cause the polynomial function to be (a) zero, (b) positive, and (c) negative.
-
(Multiple Choice)
4.7/5  (36)
(36)
Use the Factor Theorem to determine whether the first polynomial is a factor of the second polynomial.
-
(Multiple Choice)
4.8/5  (35)
(35)
Solve the problem.
-A retailer knows that games can be sold in a month if the price is dollars per game. If he buys each game for , and if he wishes to make a profit of at least per month on sales of this game, how many games must he sell each month?
(Multiple Choice)
4.9/5  (30)
(30)
Use synthetic division to determine whether the number k is an upper or lower bound (as specified) for the real zeros of
the function f.
- Lower bound?
(True/False)
4.9/5  (46)
(46)
Solve the problem.
-An open-top rectangular box has a square base and it will hold 256 cubic centimeters (cc). Each side has length height . The box's surface area is given by
Estimate the minimum surface area and the value of that will yield it.
(Multiple Choice)
4.8/5  (28)
(28)
If the following is a polynomial function, then state its degree and leading coefficient. If it is not, then state this fact.
-
(Multiple Choice)
4.8/5  (35)
(35)
Solve the problem. Round as appropriate.
-The weight of a liquid varies directly as its volume V. If the weight of the liquid in a cubical container 3 cm on a side is 81 g, find the weight of the liquid in a cubical container 4 cm on a side.
(Multiple Choice)
5.0/5  (35)
(35)
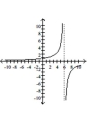
Match the graph of the rational function with its equation.
-
(Multiple Choice)
4.8/5  (41)
(41)
Graph the function in a viewing window that shows all of its extrema and x-intercepts.
-
(Multiple Choice)
4.8/5  (28)
(28)
Write the word or phrase that best completes each statement or answers the question.
Write a sentence that expresses the relationship in the formula, using the language of variation or proportion.
-
(Essay)
4.8/5  (40)
(40)
If the following is a polynomial function, then state its degree and leading coefficient. If it is not, then state this fact.
-
(Multiple Choice)
4.9/5  (38)
(38)
Write a polynomial function of minimum degree with real coefficients whose zeros include those listed. Write the
polynomial in standard form.
-1 and
(Multiple Choice)
4.8/5  (41)
(41)
Use a cubic or quartic regression (as specified) to fit a curve through the points given in the table. Round to the nearest
hundredth.
-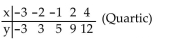
(Multiple Choice)
4.9/5  (32)
(32)
Write an equation for the linear function f satisfying the given conditions.
- and
(Multiple Choice)
4.9/5  (34)
(34)
Showing 221 - 240 of 494
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)