Exam 13: Introduction to Multiple Regression

TABLE 13-15 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily mean of the percentage of students attending class (% Attendance), mean teacher salary in dollars (Salaries), and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Following is the multiple regression output with Y = % Passing as the dependent variable, 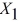= : % Attendance, 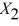= Salaries and 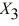= Spending: 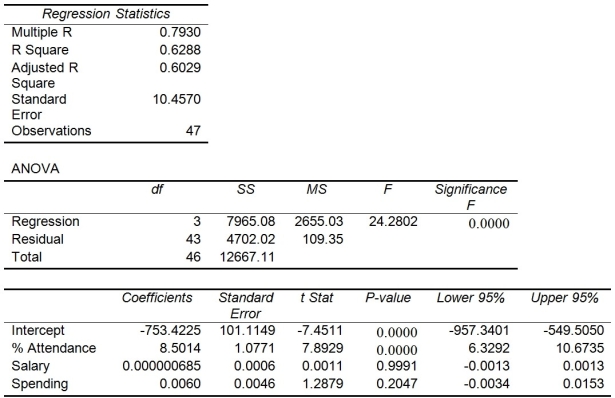-Referring to Table 13-15, there is sufficient evidence that instructional spending per pupil has an effect on percentage of students passing the proficiency test, while holding constant the effect of all the other independent variables at a 5% level of significance.

TABLE 13-6 One of the most common questions of prospective house buyers pertains to the cost of heating in dollars (Y). To provide its customers with information on that matter, a large real estate firm used the following four variables to predict heating costs: the daily minimum outside temperature in degrees of Fahrenheit (X1), the amount of insulation in inches (X2), the number of windows in the house (X3), and the age of the furnace in years (X4). Given below are the Microsoft Excel outputs of two regression models. 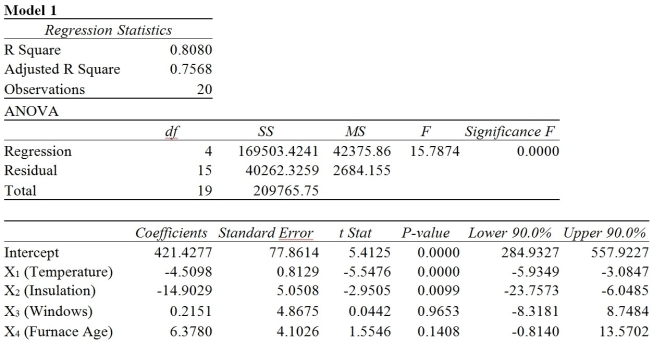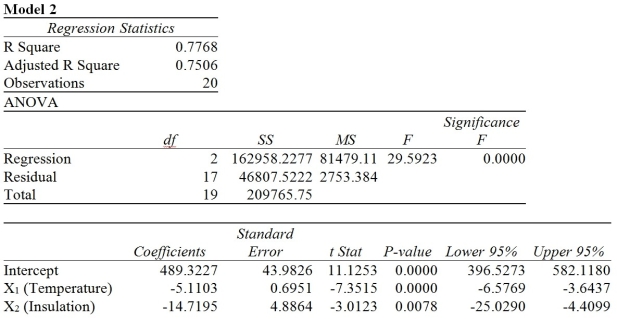-A regression had the following results: SST = 102.55, SSE = 82.04. It can be said that 90.0% of the variation in the dependent variable is explained by the independent variables in the regression.

TABLE 13-9 You decide to predict gasoline prices in different cities and towns in the United States for your term project. Your dependent variable is price of gasoline per gallon and your explanatory variables are per capita income, the number of firms that manufacture automobile parts in and around the city, the number of new business starts in the last year, population density of the city, percentage of local taxes on gasoline, and the number of people using public transportation. You collected data of 32 cities and obtained a regression sum of squares SSR= 122.8821. Your computed value of standard error of the estimate is 1.9549. -Referring to Table 13-9, the value of adjusted r² is ________.

TABLE 13-15 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily mean of the percentage of students attending class (% Attendance), mean teacher salary in dollars (Salaries), and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Following is the multiple regression output with Y = % Passing as the dependent variable, 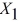= : % Attendance, 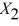= Salaries and 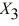= Spending: -Referring to Table 13-15, you can conclude that average teacher salary individually has no impact on the mean percentage of students passing the proficiency test, taking into account the effect of all the other independent variables, at a 10% level of significance based solely on the 95% confidence interval estimate for β₂.

TABLE 13-17 Given below are results from the regression analysis where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Unemploy) and the independent variables are the age of the worker (Age), the number of years of education received (Edu), the number of years at the previous job (Job Yr), a dummy variable for marital status (Married: 1 = married, 0 = otherwise), a dummy variable for head of household (Head: 1 = yes, 0 = no) and a dummy variable for management position (Manager: 1 = yes, 0 = no). We shall call this Model 1. 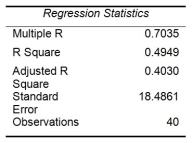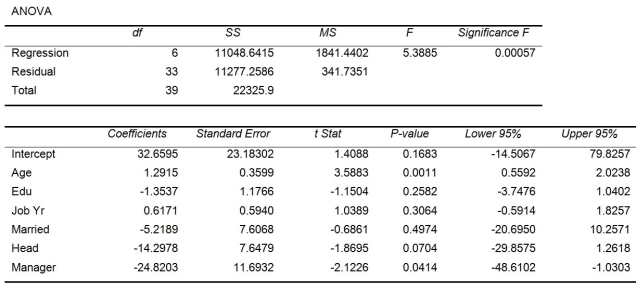Model 2 is the regression analysis where the dependent variable is Unemploy and the independent variables are Age and Manager. 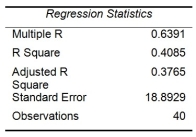The results of the regression analysis are given below: 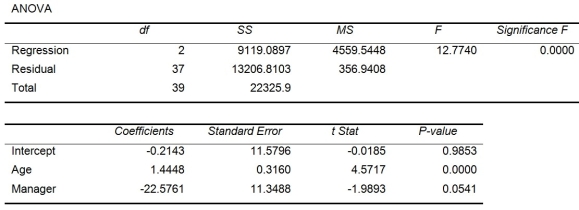-Referring to Table 13-17 Model 1, which of the following is the correct alternative hypothesis to test whether age has any effect on the number of weeks a worker is unemployed due to a layoff, while holding constant the effect of all the other independent variables?

TABLE 13-15 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily mean of the percentage of students attending class (% Attendance), mean teacher salary in dollars (Salaries), and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Following is the multiple regression output with Y = % Passing as the dependent variable, 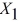= : % Attendance, 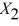= Salaries and 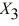= Spending: -Referring to Table 13-15, what are the lower and upper limits of the 95% confidence interval estimate for the effect of a one dollar increase in mean teacher salary on the mean percentage of students passing the proficiency test?

TABLE 13-2 A professor of industrial relations believes that an individual's wage rate at a factory (Y) depends on his performance rating (X1) and the number of economics courses the employee successfully completed in college (X2). The professor randomly selects six workers and collects the following information: 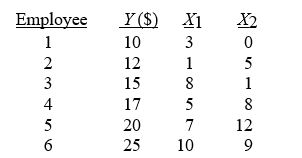-The variation attributable to factors other than the relationship between the independent variables and the explained variable in a regression analysis is represented by

TABLE 13-6 One of the most common questions of prospective house buyers pertains to the cost of heating in dollars (Y). To provide its customers with information on that matter, a large real estate firm used the following four variables to predict heating costs: the daily minimum outside temperature in degrees of Fahrenheit (X1), the amount of insulation in inches (X2), the number of windows in the house (X3), and the age of the furnace in years (X4). Given below are the Microsoft Excel outputs of two regression models. -You have just computed a regression model in which the value of coefficient of multiple determination is 0.57. To determine if this indicates that the independent variables explain a significant portion of the variation in the dependent variable, you would perform an F test.

TABLE 13-15 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily mean of the percentage of students attending class (% Attendance), mean teacher salary in dollars (Salaries), and instructional spending per pupil in dollars (Spending) of 47 schools in the state. Following is the multiple regression output with Y = % Passing as the dependent variable, 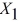= : % Attendance, 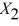= Salaries and 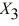= Spending: -Referring to Table 13-15, there is sufficient evidence that daily mean of the percentage of students attending class has an effect on percentage of students passing the proficiency test, while holding constant the effect of all the other independent variables at a 5% level of significance.

The coefficient of multiple determination r²Y.₁₂

TABLE 13-4 A real estate builder wishes to determine how house size (House) is influenced by family income (Income), family size (Size), and education of the head of household (School). House size is measured in hundreds of square feet, income is measured in thousands of dollars, and education is in years. The builder randomly selected 50 families and ran the multiple regression. Microsoft Excel output is provided below: 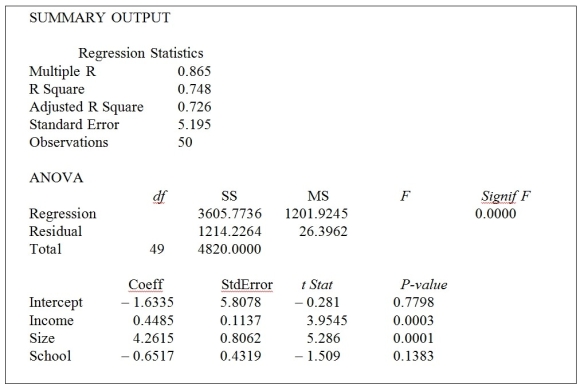-Referring to Table 13-4, what are the regression degrees of freedom that are missing from the output?