Exam 13: Introduction to Multiple Regression
Exam 1: Introduction118 Questions
Exam 2: Organizing and Visualizing Data210 Questions
Exam 3: Numerical Descriptive Measures143 Questions
Exam 4: Basic Probability171 Questions
Exam 5: Discrete Probability Distributions137 Questions
Exam 6: The Normal Distribution145 Questions
Exam 7: Sampling and Sampling Distributions197 Questions
Exam 8: Confidence Interval Estimation185 Questions
Exam 9: Fundamentals of Hypothesis Testing: One-Sample Tests168 Questions
Exam 10: Two-Sample Tests and One-Way ANOVA293 Questions
Exam 11: Chi-Square Tests108 Questions
Exam 12: Simple Linear Regression213 Questions
Exam 13: Introduction to Multiple Regression291 Questions
Exam 14: Statistical Applications in Quality Management107 Questions
Select questions type
TABLE 13-15
The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily mean of the percentage of students attending class (% Attendance), mean teacher salary in dollars (Salaries), and instructional spending per pupil in dollars (Spending) of 47 schools in the state.
Following is the multiple regression output with Y = % Passing as the dependent variable, 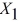 = : % Attendance,
= : % Attendance, 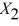 = Salaries and
= Salaries and 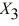 = Spending:
= Spending:
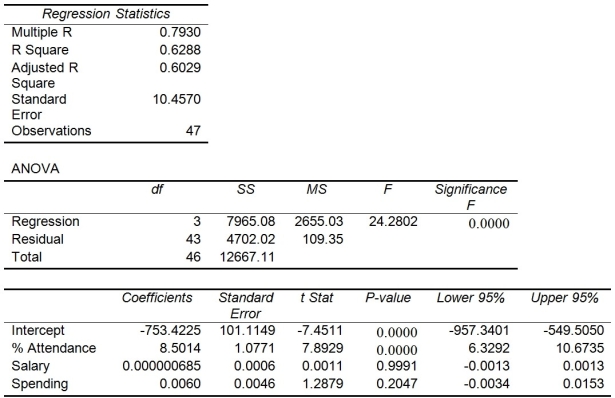 -Referring to Table 13-15, estimate the mean percentage of students passing the proficiency test for all the schools that have a daily mean of 95% of students attending class, an mean teacher salary of 40,000 dollars, and an instructional spending per pupil of 2,000 dollars.
-Referring to Table 13-15, estimate the mean percentage of students passing the proficiency test for all the schools that have a daily mean of 95% of students attending class, an mean teacher salary of 40,000 dollars, and an instructional spending per pupil of 2,000 dollars.
(Short Answer)
4.8/5  (33)
(33)
TABLE 13-6
One of the most common questions of prospective house buyers pertains to the cost of heating in dollars (Y). To provide its customers with information on that matter, a large real estate firm used the following four variables to predict heating costs: the daily minimum outside temperature in degrees of Fahrenheit (X1), the amount of insulation in inches (X2), the number of windows in the house (X3), and the age of the furnace in years (X4). Given below are the Microsoft Excel outputs of two regression models.
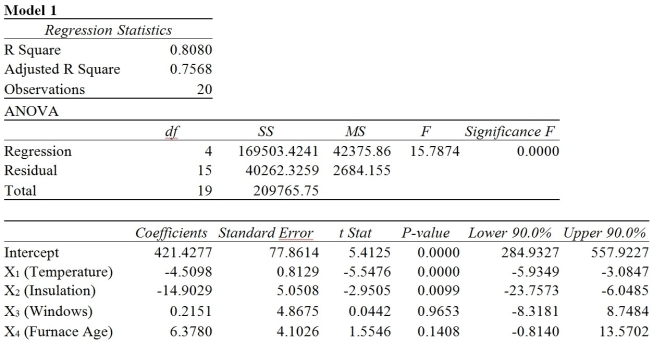
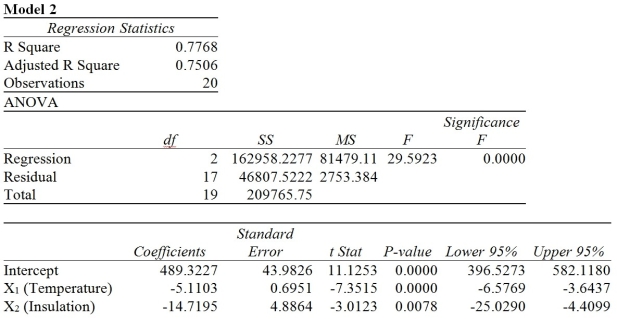 -The interpretation of the slope is different in a multiple linear regression model as compared to a simple linear regression model.
-The interpretation of the slope is different in a multiple linear regression model as compared to a simple linear regression model.
(True/False)
5.0/5  (40)
(40)
TABLE 13-9
You decide to predict gasoline prices in different cities and towns in the United States for your term project. Your dependent variable is price of gasoline per gallon and your explanatory variables are per capita income, the number of firms that manufacture automobile parts in and around the city, the number of new business starts in the last year, population density of the city, percentage of local taxes on gasoline, and the number of people using public transportation. You collected data of 32 cities and obtained a regression sum of squares SSR= 122.8821. Your computed value of standard error of the estimate is 1.9549.
-Referring to Table 13-9, if variables that measure the number of new business starts in the last year and population density of the city were removed from the multiple regression model, which of the following would be true?
(Multiple Choice)
4.8/5  (37)
(37)
TABLE 13-7
The department head of the accounting department wanted to see if she could predict the GPA of students using the number of course units (credits) and total SAT scores of each. She takes a sample of students and generates the following Microsoft Excel output:
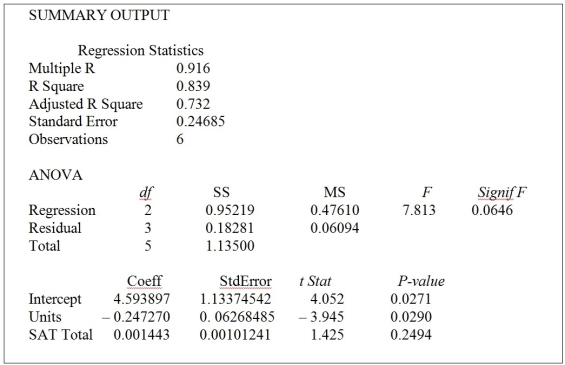 -Referring to Table 13-7, the department head wants to test H₀: β₁ = β₂ = 0. The appropriate alternative hypothesis is ________.
-Referring to Table 13-7, the department head wants to test H₀: β₁ = β₂ = 0. The appropriate alternative hypothesis is ________.
(Short Answer)
4.9/5  (36)
(36)
TABLE 13-11
A weight-loss clinic wants to use regression analysis to build a model for weight loss of a client (measured in pounds). Two variables thought to affect weight loss are client's length of time on the weight loss program and time of session. These variables are described below:
Y = Weight loss (in pounds)
X1 = Length of time in weight-loss program (in months)
X2 = 1 if morning session, 0 if not
X3 = 1 if afternoon session, 0 if not (Base level = evening session)
Data for 12 clients on a weight-loss program at the clinic were collected and used to fit the interaction model:
Y = β0 + β1X1 + β2X2 + β3X3 + β4X1X2 + β5X1X3 + ε
Partial output from Microsoft Excel follows:
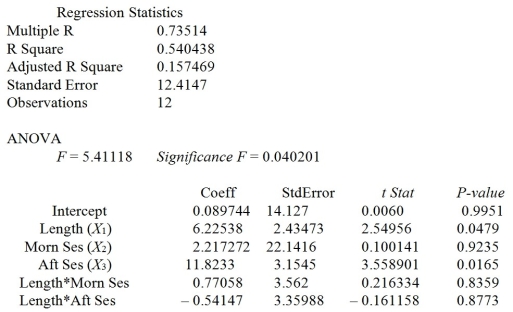 -Referring to Table 13-11, in terms of the βs in the model, give the mean change in weight loss (Y)for every one-month increase in time in the program (X₁)when attending the evening session.
-Referring to Table 13-11, in terms of the βs in the model, give the mean change in weight loss (Y)for every one-month increase in time in the program (X₁)when attending the evening session.
(Multiple Choice)
4.8/5  (36)
(36)
TABLE 13-15
The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily mean of the percentage of students attending class (% Attendance), mean teacher salary in dollars (Salaries), and instructional spending per pupil in dollars (Spending) of 47 schools in the state.
Following is the multiple regression output with Y = % Passing as the dependent variable, 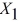 = : % Attendance,
= : % Attendance, 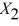 = Salaries and
= Salaries and 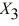 = Spending:
= Spending:
 -Referring to Table 13-15, what are the numerator and denominator degrees of freedom, respectively, for the test statistic to determine whether there is a significant relationship between percentage of students passing the proficiency test and the entire set of explanatory variables?
-Referring to Table 13-15, what are the numerator and denominator degrees of freedom, respectively, for the test statistic to determine whether there is a significant relationship between percentage of students passing the proficiency test and the entire set of explanatory variables?
(Short Answer)
4.8/5  (36)
(36)
TABLE 13-15
The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily mean of the percentage of students attending class (% Attendance), mean teacher salary in dollars (Salaries), and instructional spending per pupil in dollars (Spending) of 47 schools in the state.
Following is the multiple regression output with Y = % Passing as the dependent variable, 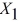 = : % Attendance,
= : % Attendance, 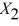 = Salaries and
= Salaries and 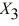 = Spending:
= Spending:
 -Referring to Table 13-15, which of the following is the correct alternative hypothesis to determine whether there is a significant relationship between percentage of students passing the proficiency test and the entire set of explanatory variables?
-Referring to Table 13-15, which of the following is the correct alternative hypothesis to determine whether there is a significant relationship between percentage of students passing the proficiency test and the entire set of explanatory variables?
(Multiple Choice)
4.9/5  (32)
(32)
TABLE 13-8
A financial analyst wanted to examine the relationship between salary (in $1,000) and four variables: age (X1 = Age), experience in the field (X2 = Exper), number of degrees (X3 = Degrees), and number of previous jobs in the field (X4 = Prevjobs). He took a sample of 20 employees and obtained the following Microsoft Excel output:
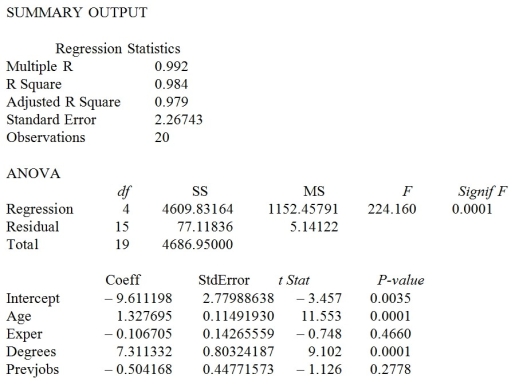 -Referring to Table 13-8, the critical value of an F test on the entire regression for a level of significance of 0.01 is ________.
-Referring to Table 13-8, the critical value of an F test on the entire regression for a level of significance of 0.01 is ________.
(Short Answer)
4.9/5  (39)
(39)
TABLE 13-17
Given below are results from the regression analysis where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Unemploy) and the independent variables are the age of the worker (Age), the number of years of education received (Edu), the number of years at the previous job (Job Yr), a dummy variable for marital status (Married: 1 = married, 0 = otherwise), a dummy variable for head of household (Head: 1 = yes, 0 = no) and a dummy variable for management position (Manager: 1 = yes, 0 = no). We shall call this Model 1.
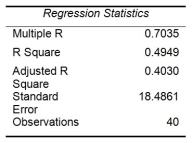
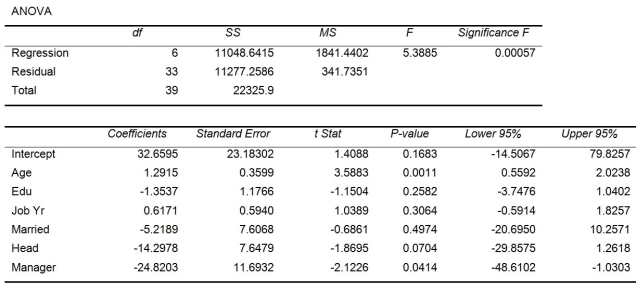 Model 2 is the regression analysis where the dependent variable is Unemploy and the independent variables are Age and Manager. The results of the regression analysis are given below:
Model 2 is the regression analysis where the dependent variable is Unemploy and the independent variables are Age and Manager. The results of the regression analysis are given below:
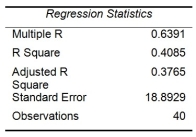
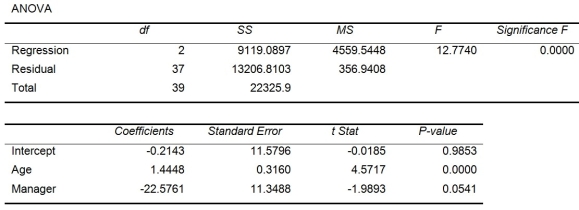 -Referring to Table 13-17 Model 1, the null hypothesis H₀: β₁ = β₂ = β₃ = β₄ = β₅ = β₆ = 0 implies that the number of weeks a worker is unemployed due to a layoff is not related to any of the explanatory variables.
-Referring to Table 13-17 Model 1, the null hypothesis H₀: β₁ = β₂ = β₃ = β₄ = β₅ = β₆ = 0 implies that the number of weeks a worker is unemployed due to a layoff is not related to any of the explanatory variables.
(True/False)
4.8/5  (39)
(39)
TABLE 13-16
What are the factors that determine the acceleration time (in sec.) from 0 to 60 miles per hour of a car? Data on the following variables for 171 different vehicle models were collected:
Accel Time: Acceleration time in sec.
Cargo Vol: Cargo volume in cu. ft.
HP: Horsepower
MPG: Miles per gallon
SUV: 1 if the vehicle model is an SUV with Coupe as the base when SUV and Sedan are both 0
Sedan: 1 if the vehicle model is a sedan with Coupe as the base when SUV and Sedan are both 0
The regression results using acceleration time as the dependent variable and the remaining variables as the independent variables are presented below.
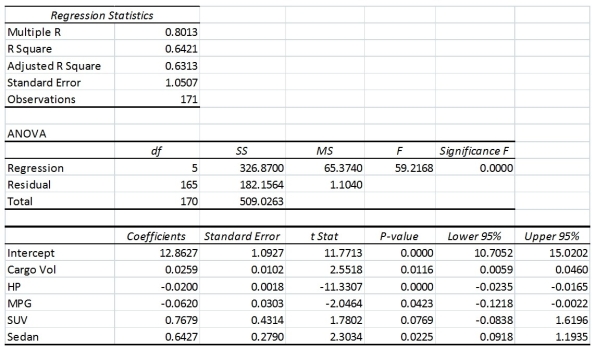 The various residual plots are as shown below.
The various residual plots are as shown below.
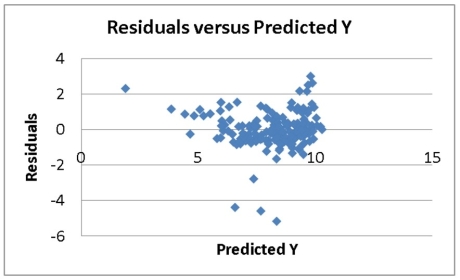
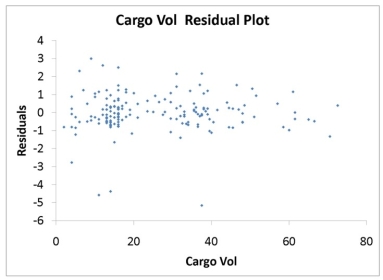
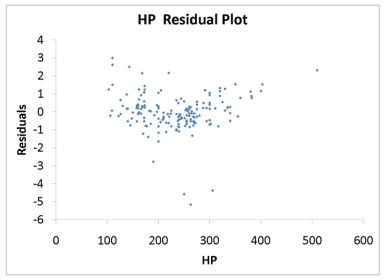
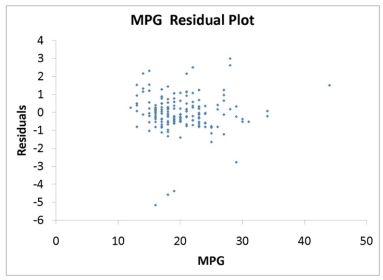
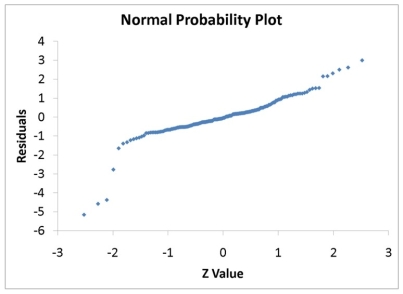 The coefficient of multiple determination for the regression model using each of the 5 variables Xj as the dependent variable and all other X variables as independent variables (Rj2) are, respectively, 0.7461, 0.5676, 0.6764, 0.8582, 0.6632.
-Referring to Table 13-16, what is the value of the test statistic to determine whether SUV makes a significant contribution to the regression model in the presence of the other independent variables at a 5% level of significance?
The coefficient of multiple determination for the regression model using each of the 5 variables Xj as the dependent variable and all other X variables as independent variables (Rj2) are, respectively, 0.7461, 0.5676, 0.6764, 0.8582, 0.6632.
-Referring to Table 13-16, what is the value of the test statistic to determine whether SUV makes a significant contribution to the regression model in the presence of the other independent variables at a 5% level of significance?
(Short Answer)
4.9/5  (41)
(41)
TABLE 13-17
Given below are results from the regression analysis where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Unemploy) and the independent variables are the age of the worker (Age), the number of years of education received (Edu), the number of years at the previous job (Job Yr), a dummy variable for marital status (Married: 1 = married, 0 = otherwise), a dummy variable for head of household (Head: 1 = yes, 0 = no) and a dummy variable for management position (Manager: 1 = yes, 0 = no). We shall call this Model 1.

 Model 2 is the regression analysis where the dependent variable is Unemploy and the independent variables are Age and Manager. The results of the regression analysis are given below:
Model 2 is the regression analysis where the dependent variable is Unemploy and the independent variables are Age and Manager. The results of the regression analysis are given below:

 -Referring to Table 13-17 Model 1, what are the numerator and denominator degrees of freedom, respectively, for the test statistic to determine whether there is a significant relationship between the number of weeks a worker is unemployed due to a layoff and the entire set of explanatory variables?
-Referring to Table 13-17 Model 1, what are the numerator and denominator degrees of freedom, respectively, for the test statistic to determine whether there is a significant relationship between the number of weeks a worker is unemployed due to a layoff and the entire set of explanatory variables?
(Short Answer)
4.9/5  (36)
(36)
TABLE 13-15
The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily mean of the percentage of students attending class (% Attendance), mean teacher salary in dollars (Salaries), and instructional spending per pupil in dollars (Spending) of 47 schools in the state.
Following is the multiple regression output with Y = % Passing as the dependent variable, 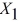 = : % Attendance,
= : % Attendance, 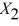 = Salaries and
= Salaries and 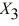 = Spending:
= Spending:
 -Referring to Table 13-15, the alternative hypothesis H₁: At least one of βⱼ ≠ 0 for j = 1, 2, 3 implies that percentage of students passing the proficiency test is related to at least one of the explanatory variables.
-Referring to Table 13-15, the alternative hypothesis H₁: At least one of βⱼ ≠ 0 for j = 1, 2, 3 implies that percentage of students passing the proficiency test is related to at least one of the explanatory variables.
(True/False)
4.9/5  (35)
(35)
TABLE 13-15
The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily mean of the percentage of students attending class (% Attendance), mean teacher salary in dollars (Salaries), and instructional spending per pupil in dollars (Spending) of 47 schools in the state.
Following is the multiple regression output with Y = % Passing as the dependent variable, 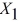 = : % Attendance,
= : % Attendance, 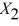 = Salaries and
= Salaries and 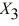 = Spending:
= Spending:
 -Referring to Table 13-15, the null hypothesis should be rejected at a 5% level of significance when testing whether there is a significant relationship between percentage of students passing the proficiency test and the entire set of explanatory variables.
-Referring to Table 13-15, the null hypothesis should be rejected at a 5% level of significance when testing whether there is a significant relationship between percentage of students passing the proficiency test and the entire set of explanatory variables.
(True/False)
4.9/5  (38)
(38)
TABLE 13-9
You decide to predict gasoline prices in different cities and towns in the United States for your term project. Your dependent variable is price of gasoline per gallon and your explanatory variables are per capita income, the number of firms that manufacture automobile parts in and around the city, the number of new business starts in the last year, population density of the city, percentage of local taxes on gasoline, and the number of people using public transportation. You collected data of 32 cities and obtained a regression sum of squares SSR= 122.8821. Your computed value of standard error of the estimate is 1.9549.
-Referring to Table 13-9, what is the value of the coefficient of multiple determination?
(Multiple Choice)
4.7/5  (37)
(37)
TABLE 13-15
The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily mean of the percentage of students attending class (% Attendance), mean teacher salary in dollars (Salaries), and instructional spending per pupil in dollars (Spending) of 47 schools in the state.
Following is the multiple regression output with Y = % Passing as the dependent variable,  = : % Attendance,
= : % Attendance, 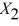 = Salaries and
= Salaries and 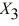 = Spending:
= Spending:
 -Referring to Table 13-15, you can conclude that mean teacher salary individually has no impact on the mean percentage of students passing the proficiency test, taking into account the effect of all the other independent variables, at a 1% level of significance based solely on the 95% confidence interval estimate for β₂.
-Referring to Table 13-15, you can conclude that mean teacher salary individually has no impact on the mean percentage of students passing the proficiency test, taking into account the effect of all the other independent variables, at a 1% level of significance based solely on the 95% confidence interval estimate for β₂.
(True/False)
4.9/5  (32)
(32)
TABLE 13-15
The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily mean of the percentage of students attending class (% Attendance), mean teacher salary in dollars (Salaries), and instructional spending per pupil in dollars (Spending) of 47 schools in the state.
Following is the multiple regression output with Y = % Passing as the dependent variable, 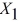 = : % Attendance,
= : % Attendance, 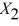 = Salaries and
= Salaries and 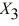 = Spending:
= Spending:
 -Referring to Table 13-15, the alternative hypothesis H₁: At least one of βⱼ ≠ 0 for j = 1, 2, 3 implies that percentage of students passing the proficiency test is related to all of the explanatory variables.
-Referring to Table 13-15, the alternative hypothesis H₁: At least one of βⱼ ≠ 0 for j = 1, 2, 3 implies that percentage of students passing the proficiency test is related to all of the explanatory variables.
(True/False)
4.9/5  (35)
(35)
TABLE 13-11
A weight-loss clinic wants to use regression analysis to build a model for weight loss of a client (measured in pounds). Two variables thought to affect weight loss are client's length of time on the weight loss program and time of session. These variables are described below:
Y = Weight loss (in pounds)
X1 = Length of time in weight-loss program (in months)
X2 = 1 if morning session, 0 if not
X3 = 1 if afternoon session, 0 if not (Base level = evening session)
Data for 12 clients on a weight-loss program at the clinic were collected and used to fit the interaction model:
Y = β0 + β1X1 + β2X2 + β3X3 + β4X1X2 + β5X1X3 + ε
Partial output from Microsoft Excel follows:
 -Referring to Table 13-11, which of the following statements is supported by the analysis shown?
-Referring to Table 13-11, which of the following statements is supported by the analysis shown?
(Multiple Choice)
4.8/5  (35)
(35)
TABLE 13-17
Given below are results from the regression analysis where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Unemploy) and the independent variables are the age of the worker (Age), the number of years of education received (Edu), the number of years at the previous job (Job Yr), a dummy variable for marital status (Married: 1 = married, 0 = otherwise), a dummy variable for head of household (Head: 1 = yes, 0 = no) and a dummy variable for management position (Manager: 1 = yes, 0 = no). We shall call this Model 1.

 Model 2 is the regression analysis where the dependent variable is Unemploy and the independent variables are Age and Manager. The results of the regression analysis are given below:
Model 2 is the regression analysis where the dependent variable is Unemploy and the independent variables are Age and Manager. The results of the regression analysis are given below:

 -Referring to Table 13-17 Model 1, which of the following is the correct null hypothesis to determine whether there is a significant relationship between the number of weeks a worker is unemployed due to a layoff and the entire set of explanatory variables?
-Referring to Table 13-17 Model 1, which of the following is the correct null hypothesis to determine whether there is a significant relationship between the number of weeks a worker is unemployed due to a layoff and the entire set of explanatory variables?
(Multiple Choice)
4.8/5  (35)
(35)
TABLE 13-4
A real estate builder wishes to determine how house size (House) is influenced by family income (Income), family size (Size), and education of the head of household (School). House size is measured in hundreds of square feet, income is measured in thousands of dollars, and education is in years. The builder randomly selected 50 families and ran the multiple regression. Microsoft Excel output is provided below:
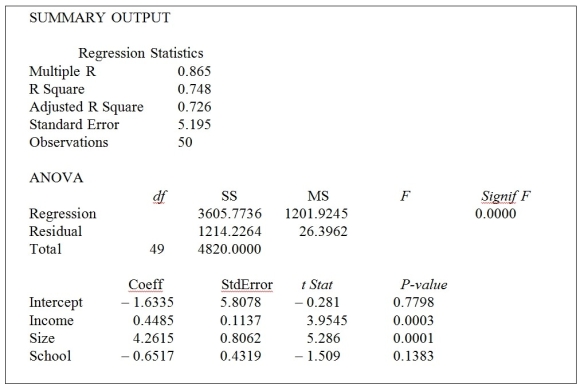 -Referring to Table 13-4, which of the following values for the level of significance is the smallest for which at least two explanatory variables are significant individually?
-Referring to Table 13-4, which of the following values for the level of significance is the smallest for which at least two explanatory variables are significant individually?
(Multiple Choice)
4.8/5  (35)
(35)
TABLE 13-3
An economist is interested to see how consumption for an economy (in $billions) is influenced by gross domestic product ($billions) and aggregate price (consumer price index). The Microsoft Excel output of this regression is partially reproduced below.
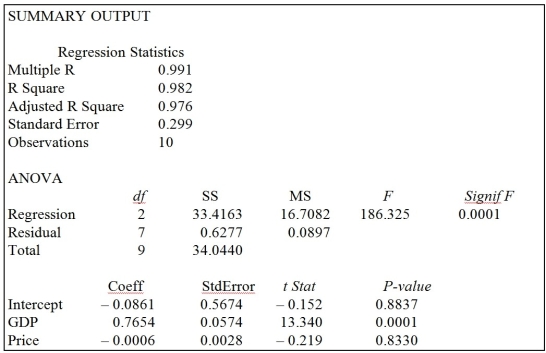 -Referring to Table 13-3, one economy in the sample had an aggregate consumption level of $4 billion, a GDP of $6 billion, and an aggregate price level of 200. What is the residual for this data point?
-Referring to Table 13-3, one economy in the sample had an aggregate consumption level of $4 billion, a GDP of $6 billion, and an aggregate price level of 200. What is the residual for this data point?
(Multiple Choice)
4.9/5  (37)
(37)
Showing 81 - 100 of 291
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)