Exam 3: Differentiation
Exam 1: Functions124 Questions
Exam 2: Limits and Derivatives213 Questions
Exam 3: Differentiation183 Questions
Exam 4: Applications of Derivatives159 Questions
Exam 5: Integration107 Questions
Exam 6: Applications of Definite Integrals115 Questions
Exam 7: Integrals and Transcendental Functions114 Questions
Exam 8: Techniques of Integration124 Questions
Exam 9: First-Order Differential Equations75 Questions
Exam 10: Infinite Sequences and Series155 Questions
Select questions type
Find the slope of the curve at the indicated point.
-A balloon used in surgical procedures is cylindrical in shape. As it expands outward, assume that the length remains a constant . Find the rate of change of surface area with respect to radius when the radius is . (Answer can be left in terms of ).
(Multiple Choice)
4.9/5  (39)
(39)
Find an equation for the tangent to the curve at the given point.
-
(Multiple Choice)
4.9/5  (42)
(42)
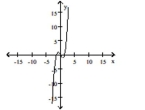
The graph of a function is given. Choose the answer that represents the graph of its derivative
-
(Multiple Choice)
4.9/5  (36)
(36)
Suppose u and v are differentiable functions of x. Use the given values of the functions and their derivatives to find the value of the indicated derivative.
- u(2)=10,(2)=2,v(2)=-1,(2)=-4 (3v-u) at x=2
(Multiple Choice)
4.9/5  (40)
(40)
Find an equation for the tangent to the curve at the given point.
-
(Multiple Choice)
4.9/5  (31)
(31)
Provide an appropriate response.
-Under standard conditions, molecules of a gas collide billions of times per second. If each molecule has diameter average distance between collisions is given by
where , the volume density of the gas, is a constant. Find .
(Multiple Choice)
4.8/5  (48)
(48)
Provide an appropriate response.
-Is there any difference between finding the derivative of f(x) at x = a and finding the slope of the line tangent to f(x) at x = a? Explain.
(Essay)
4.9/5  (43)
(43)
Given the graph of f, find any values of x at which f ' is not defined.
-The graph of y = f(x) in the accompanying figure is made of line segments joined end to end. Graph the derivative of f.
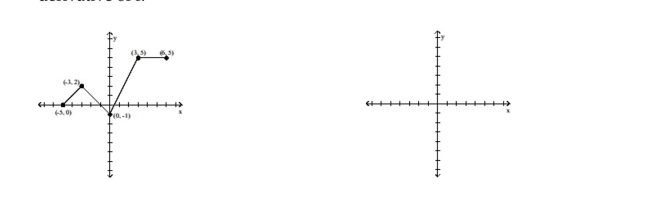
(Multiple Choice)
4.8/5  (34)
(34)
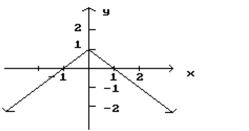
Given the graph of f, find any values of x at which f ' is not defined.
-
(Multiple Choice)
4.9/5  (37)
(37)
Suppose u and v are differentiable functions of x. Use the given values of the functions and their derivatives to find the value of the indicated derivative.
- u(2)=6,(2)=3,v(2)=-1,(2)=-4. at x=2
(Multiple Choice)
4.8/5  (45)
(45)
Suppose u and v are differentiable functions of x. Use the given values of the functions and their derivatives to find the value of the indicated derivative.
-
at
(Multiple Choice)
4.7/5  (36)
(36)
Calculate the derivative of the function. Then find the value of the derivative as specified.
-
(Multiple Choice)
4.8/5  (36)
(36)
Suppose u and v are differentiable functions of x. Use the given values of the functions and their derivatives to find the value of the indicated derivative.
-
at
(Multiple Choice)
4.9/5  (39)
(39)
Provide an appropriate response.
-Over what intervals of x-values, if any, does the function y increase as x increases? For what values of x, if any, is y' positive? How are your answers related?
(Essay)
4.9/5  (33)
(33)
Showing 41 - 60 of 183
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)