Question 1

Find the second derivative of the function.
-$$r = \left( \frac { 1 + 8 \theta } { 8 \theta } \right) ( 8 - \theta )$$

Accepted Answer

A)  $\frac { \mathrm { d } ^ { 2 } r } { d \theta ^ { 2 } } = \frac { 2 } { \theta ^ { 3 } }$ 
B)  $\frac { \mathrm { d } ^ { 2 } r } { d \theta ^ { 2 } } = \frac { 1 } { \theta } - \theta$ 
C)  $\frac { d ^ { 2 } r } { d \theta ^ { 2 } } = - \frac { 2 } { \theta ^ { 3 } } - 1$ 
D)  $\frac { d ^ { 2 } r } { d \theta ^ { 2 } } = - \frac { 1 } { \theta ^ { 2 } } - 1$ 
A)  $\frac { \mathrm { d } ^ { 2 } r } { d \theta ^ { 2 } } = \frac { 2 } { \theta ^ { 3 } }$ 
B)  $\frac { \mathrm { d } ^ { 2 } r } { d \theta ^ { 2 } } = \frac { 1 } { \theta } - \theta$ 
C)  $\frac { d ^ { 2 } r } { d \theta ^ { 2 } } = - \frac { 2 } { \theta ^ { 3 } } - 1$ 
D)  $\frac { d ^ { 2 } r } { d \theta ^ { 2 } } = - \frac { 1 } { \theta ^ { 2 } } - 1$

Question 2

Find y'.
-$$y = \left( \frac { 6 } { x } + x \right) \left( \frac { 6 } { x } - x \right)$$

Accepted Answer

A)  $\frac { 72 } { x ^ { 3 } } + 2 x$ 
B)  $- \frac { 72 } { x } + 2 x$ 
C)  $- \frac { 36 } { x ^ { 3 } } - 2 x$ 
D)  $- \frac { 72 } { x ^ { 3 } } - 2 x$ 
A)  $\frac { 72 } { x ^ { 3 } } + 2 x$ 
B)  $- \frac { 72 } { x } + 2 x$ 
C)  $- \frac { 36 } { x ^ { 3 } } - 2 x$ 
D)  $- \frac { 72 } { x ^ { 3 } } - 2 x$

Question 3

Find the slope of the curve at the indicated point.
-Find the points where the graph of the function have horizontal tangents.
$$f ( x ) = x ^ { 3 } - 15 x$$

Accepted Answer

A)  $( \sqrt { 5 } , - 30 \sqrt { 5 } )$ 
B)  $( - 5 , - 50 ) , ( \sqrt { 5 } , 50 )$ 
C)  $( - \sqrt { 5 } , 30 \sqrt { 5 } ) , ( 0,0 ) , ( \sqrt { 5 } , - 30 \sqrt { 5 } )$ 
D)  $( - \sqrt { 5 } , 10 \sqrt { 5 } ) , ( \sqrt { 5 } , - 10 \sqrt { 5 } )$ 
A)  $( \sqrt { 5 } , - 30 \sqrt { 5 } )$ 
B)  $( - 5 , - 50 ) , ( \sqrt { 5 } , 50 )$ 
C)  $( - \sqrt { 5 } , 30 \sqrt { 5 } ) , ( 0,0 ) , ( \sqrt { 5 } , - 30 \sqrt { 5 } )$ 
D)  $( - \sqrt { 5 } , 10 \sqrt { 5 } ) , ( \sqrt { 5 } , - 10 \sqrt { 5 } )$

Question 4

Provide an appropriate response.
-A charged particle of mass $m$ and charge $q$ moving in an electric field $E$ has an acceleration a given by $\mathrm { a } = \frac { \mathrm { qE } } { \mathrm { m } }$,
where $\mathrm { q }$ and $\mathrm { E }$ are constants. Find $\frac { \mathrm { d } ^ { 2 } \mathrm { a } } { \mathrm { dm } ^ { 2 } }$.

Accepted Answer

A)  $\frac { \mathrm { d } ^ { 2 } \mathrm { a } } { \mathrm { dm^{2 } } = - \frac { \mathrm { qE } } { \mathrm { m } ^ { 2 } } }$ 
B)  $\frac { \mathrm { d } ^ { 2 } \mathrm { a } } { d \mathrm {~m} ^ { 2 } } = \frac { \mathrm { q } E } { 2 \mathrm {~m} }$ 
C)  $\frac { d ^ { 2 } a } { d m ^ { 2 } } = \frac { 2 q E } { m ^ { 3 } }$ 
D)  $\frac { \mathrm { d } ^ { 2 } \mathrm { a } } { d \mathrm {~m} ^ { 2 } } = \frac { \mathrm { qE } } { \mathrm { m } ^ { 3 } }$ 
A)  $\frac { \mathrm { d } ^ { 2 } \mathrm { a } } { \mathrm { dm^{2 } } = - \frac { \mathrm { qE } } { \mathrm { m } ^ { 2 } } }$ 
B)  $\frac { \mathrm { d } ^ { 2 } \mathrm { a } } { d \mathrm {~m} ^ { 2 } } = \frac { \mathrm { q } E } { 2 \mathrm {~m} }$ 
C)  $\frac { d ^ { 2 } a } { d m ^ { 2 } } = \frac { 2 q E } { m ^ { 3 } }$ 
D)  $\frac { \mathrm { d } ^ { 2 } \mathrm { a } } { d \mathrm {~m} ^ { 2 } } = \frac { \mathrm { qE } } { \mathrm { m } ^ { 3 } }$

Question 5

Find the slope of the curve at the indicated point.
-Find an equation of the tangent to the curve $f ( x ) = \sqrt { x + 4 }$ that has slope $\frac { 1 } { 4 }$.

Accepted Answer

A)  $y = \frac { 1 } { 4 } x$ 
B)  $y = \frac { 1 } { 4 } x + 2$ 
C)  $y = \frac { 1 } { 4 } x - 2$ 
D)  $y = - \frac { 1 } { 4 } x + 2$ 
A)  $y = \frac { 1 } { 4 } x$ 
B)  $y = \frac { 1 } { 4 } x + 2$ 
C)  $y = \frac { 1 } { 4 } x - 2$ 
D)  $y = - \frac { 1 } { 4 } x + 2$

Question 6

Find the indicated derivative.
-$\frac { d p } { d q }$ if $p = \frac { 1 } { \sqrt { q + 1 } }$

Accepted Answer

A)  $\frac { 1 } { 2 ( q + 1 ) \sqrt { q + 1 } }$ 
B)  $- \frac { 1 } { ( q + 1 ) \sqrt { q + 1 } }$ 
C)  $- \frac { 1 } { 2 \sqrt { q + 1 } }$ 
D)  $- \frac { 1 } { 2 ( q + 1 ) \sqrt { q + 1 } }$ 
A)  $\frac { 1 } { 2 ( q + 1 ) \sqrt { q + 1 } }$ 
B)  $- \frac { 1 } { ( q + 1 ) \sqrt { q + 1 } }$ 
C)  $- \frac { 1 } { 2 \sqrt { q + 1 } }$ 
D)  $- \frac { 1 } { 2 ( q + 1 ) \sqrt { q + 1 } }$

Question 7

Find the derivative.
-w = $\sqrt[3] {z^{6.6}}$ + $5e^{3.1}$

Accepted Answer

A)  2.2z1.2 + 3.1e2.1 
B)  2.2z1.2 + 15.5e3.1 
C)  2.2z1.2 + 15.5e2.1 
D)  2.2z5.6 + 15.5e2.1 
A)  2.2z1.2 + 3.1e2.1 
B)  2.2z1.2 + 15.5e3.1 
C)  2.2z1.2 + 15.5e2.1 
D)  2.2z5.6 + 15.5e2.1

Question 8

Find the slope of the curve at the indicated point.
-Find equations of all tangents to the curve $f ( x ) = \frac { 1 } { x }$ that have slope $- 1$.

Accepted Answer

A)  $y = - x + 2$ 
B)  $y = - x + 2 , y = - x - 2$ 
C)  $y = x - 2$ 
D)  $y = x + 2 , y = x - 2$ 
A)  $y = - x + 2$ 
B)  $y = - x + 2 , y = - x - 2$ 
C)  $y = x - 2$ 
D)  $y = x + 2 , y = x - 2$

Question 9

Find the second derivative.
-$$y = 2 x ^ { 3 } - 7 x ^ { 2 } + 3$$

Accepted Answer

A)  $14 x - 8$ 
B)  $12 \mathrm { x } - 14$ 
C)  $14 x - 12$ 
D)  $8 x - 14$ 
A)  $14 x - 8$ 
B)  $12 \mathrm { x } - 14$ 
C)  $14 x - 12$ 
D)  $8 x - 14$

Question 10

Find the derivative.
-$$w = z ^ { 6 - e }$$

Accepted Answer

A)  $( 5 - e ) z ^ { 6 - e }$ 
B)  $\frac { z ^ { 7 - e } } { 7 - e }$ 
C)  $( 6 - \mathrm { e } ) \mathrm { z } ^ { 5 - \mathrm { e } }$ 
D)  $z ^ { 6 - e }$ 
A)  $( 5 - e ) z ^ { 6 - e }$ 
B)  $\frac { z ^ { 7 - e } } { 7 - e }$ 
C)  $( 6 - \mathrm { e } ) \mathrm { z } ^ { 5 - \mathrm { e } }$ 
D)  $z ^ { 6 - e }$

Question 11

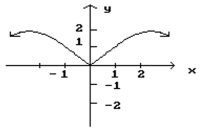
Given the graph of f, find any values of x at which f ' is not defined.
-

Accepted Answer

A)  x = -2, 0, 2 
B)  x = -2, 2 
C)  x = 0 
D)  x = 2 
A)  x = -2, 0, 2 
B)  x = -2, 2 
C)  x = 0 
D)  x = 2

Question 12

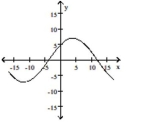
The graph of a function is given. Choose the answer that represents the graph of its derivative
-

Accepted Answer

A) 
  
B) 
  
C) 
  
D) 
  
A) 
  
B) 
  
C) 
  
D)

Question 13

Find the derivative of the function.
-$$r = \frac { \sqrt { \theta } - 8 } { \sqrt { \theta } + 8 }$$

Accepted Answer

A)  $r ^ { \prime } = - \frac { 8 } { \sqrt { \theta } ( \theta + 8 ) ^ { 2 } }$ 
B)  $\mathrm { r } ^ { \prime } = \frac { 8 } { \sqrt { \theta } ( \theta + 8 ) ^ { 2 } }$ 
C)  $r ^ { \prime } = \frac { 16 } { ( \theta + 8 ) \sqrt { \theta ^ { 2 } - 64 } }$ 
D)  $\mathrm { r } ^ { \prime } = \frac { 8 } { \theta + 8 }$ 
A)  $r ^ { \prime } = - \frac { 8 } { \sqrt { \theta } ( \theta + 8 ) ^ { 2 } }$ 
B)  $\mathrm { r } ^ { \prime } = \frac { 8 } { \sqrt { \theta } ( \theta + 8 ) ^ { 2 } }$ 
C)  $r ^ { \prime } = \frac { 16 } { ( \theta + 8 ) \sqrt { \theta ^ { 2 } - 64 } }$ 
D)  $\mathrm { r } ^ { \prime } = \frac { 8 } { \theta + 8 }$

Question 14

Provide an appropriate response.
-Under standard conditions, molecules of a gas collide billions of times per second. If each molecule has diameteı average distance between collisions is given by
$\mathrm { L } = \frac { 1 } { \sqrt { 2 } \pi \mathrm { t } ^ { 2 } \mathrm { n } }$ where $n$, the volume density of the gas, is a constant. Find $\frac { d ^ { 2 } L } { d t ^ { 2 } }$.

Accepted Answer

A)  $\frac { \mathrm { d } ^ { 2 } \mathrm {~L} } { d t ^ { 2 } } = - \frac { 2 } { \sqrt { 2 } \pi t ^ { 3 } n }$ 
B)  $\frac { d ^ { 2 } L } { d t ^ { 2 } } = \frac { 6 } { \sqrt { 2 } \pi t ^ { 4 } n }$ 
C)  $\frac { \mathrm { d } ^ { 2 } \mathrm {~L} } { \mathrm { dt } ^ { 2 } } = - \frac { 2 } { \sqrt { 2 } \pi \mathrm { t } ^ { 2 } \mathrm { n } }$ 
D)  $\frac { \mathrm { d } ^ { 2 } \mathrm {~L} } { \mathrm { dt } ^ { 2 } } = - \frac { 6 } { \sqrt { 2 } \pi t ^ { 4 } \mathrm { n } }$ 
A)  $\frac { \mathrm { d } ^ { 2 } \mathrm {~L} } { d t ^ { 2 } } = - \frac { 2 } { \sqrt { 2 } \pi t ^ { 3 } n }$ 
B)  $\frac { d ^ { 2 } L } { d t ^ { 2 } } = \frac { 6 } { \sqrt { 2 } \pi t ^ { 4 } n }$ 
C)  $\frac { \mathrm { d } ^ { 2 } \mathrm {~L} } { \mathrm { dt } ^ { 2 } } = - \frac { 2 } { \sqrt { 2 } \pi \mathrm { t } ^ { 2 } \mathrm { n } }$ 
D)  $\frac { \mathrm { d } ^ { 2 } \mathrm {~L} } { \mathrm { dt } ^ { 2 } } = - \frac { 6 } { \sqrt { 2 } \pi t ^ { 4 } \mathrm { n } }$

Question 15

Suppose u and v are differentiable functions of x. Use the given values of the functions and their derivatives to find the value of the indicated derivative.
-$$\begin{array} { l } 
u ( 2 ) = 6 , u ^ { \prime } ( 2 ) = 2 , v ( 2 ) = - 2 , v ^ { \prime } ( 2 ) = - 5 . \
\frac { d } { d x } ( 2 u - 4 v ) \text { at } x = 2
\end{array}$$

Accepted Answer

A)  $- 16$ 
B)  4 
C)  20 
D)  24 
A)  $- 16$ 
B)  4 
C)  20 
D)  24

Question 16

Find the second derivative.
-$$y = 9 x ^ { 2 } + 3 x - 7$$

Accepted Answer

A)  9 
B)  18 
C)  0 
D)  $18 x + 3$ 
A)  9 
B)  18 
C)  0 
D)  $18 x + 3$

Question 17

Graph the equation and its tangent
-$$\text { Graph } y = 4 x ^ { 2 } \text { and the tangent to the curve at the point whose } x \text {-coordinate is } - 2 \text {. }$$

Accepted Answer

A) 
  
B) 
  
C) 
  
D) 
  
A) 
  
B) 
  
C) 
  
D)

Question 18

Find the derivative of the function.
-$z = 6 x ^ { 2 } e ^ { x }$

Accepted Answer

A)  $\frac { d z } { d x } = 12 x e ^ { x } - 6 x ^ { 2 } e ^ { x }$ 
B)  $\frac { d z } { d x } = 6 x e ^ { x } + 6 x ^ { 2 } e ^ { x }$ 
C)  $\frac { d z } { d x } = 12 x e ^ { x } + 6 x ^ { 2 } e ^ { x }$ 
D)  $\frac { d z } { d x } = 6 x e ^ { x } + 12 x ^ { 2 } e ^ { x }$ 
A)  $\frac { d z } { d x } = 12 x e ^ { x } - 6 x ^ { 2 } e ^ { x }$ 
B)  $\frac { d z } { d x } = 6 x e ^ { x } + 6 x ^ { 2 } e ^ { x }$ 
C)  $\frac { d z } { d x } = 12 x e ^ { x } + 6 x ^ { 2 } e ^ { x }$ 
D)  $\frac { d z } { d x } = 6 x e ^ { x } + 12 x ^ { 2 } e ^ { x }$

Question 19

Provide an appropriate response.
-A heat engine is a device that converts thermal energy into other forms. The thermal efficiency, e, of a heat engin defined by
$e = \frac { Q _ { h } - Q _ { C } } { Q _ { h } }$ where $\mathrm { Q } _ { \mathrm { h } }$ is the heat absorbed in one cycle and $\mathrm { Q } _ { \mathrm { C } }$, the heat released into a reservoir in one cycle, is a constant. Find $\frac { \mathrm { de } } { \mathrm { dQ } _ { \mathrm { h } } }$.

Accepted Answer

A)  $\frac { d e } { d Q _ { h } } = - \frac { Q _ { C } } { Q _ { h } ^ { 2 } }$ 
B)  $\frac { \mathrm { de } } { \mathrm { dQ } \mathrm { h } } = \frac { 1 } { \mathrm { Qh } ^ { 2 } }$ 
C)  $\frac { \mathrm { de } } { \mathrm { dQ } \mathrm { h } } = \frac { \mathrm { Q } _ { \mathrm { C } } } { \mathrm { Q } _ { \mathrm { h } } { } ^ { 2 } }$ 
D)  $\frac { \mathrm { de } } { \mathrm { dQ } \mathrm { h } } = \mathrm { Q } _ { \mathrm { h } } - \mathrm { Q } _ { \mathrm { C } }$ 
A)  $\frac { d e } { d Q _ { h } } = - \frac { Q _ { C } } { Q _ { h } ^ { 2 } }$ 
B)  $\frac { \mathrm { de } } { \mathrm { dQ } \mathrm { h } } = \frac { 1 } { \mathrm { Qh } ^ { 2 } }$ 
C)  $\frac { \mathrm { de } } { \mathrm { dQ } \mathrm { h } } = \frac { \mathrm { Q } _ { \mathrm { C } } } { \mathrm { Q } _ { \mathrm { h } } { } ^ { 2 } }$ 
D)  $\frac { \mathrm { de } } { \mathrm { dQ } \mathrm { h } } = \mathrm { Q } _ { \mathrm { h } } - \mathrm { Q } _ { \mathrm { C } }$

Question 20

Provide an appropriate response.
-$$\text { Does the graph of } \mathrm { f } ( \mathrm { x } ) = \left\{ \begin{array} { l l } 
1 , & \mathrm { x }  0
\end{array} \right. \text { have a vertical tangent at the origin? Give reasons for your answer. }$$

Accepted Answer

The function is not

Find the second derivative of the function. - $r = \left( \frac { 1 + 8 \theta } { 8 \theta } \right) ( 8 - \theta )$

Find y'. - $y = \left( \frac { 6 } { x } + x \right) \left( \frac { 6 } { x } - x \right)$

Find the slope of the curve at the indicated point. -Find the points where the graph of the function have horizontal tangents. $f ( x ) = x ^ { 3 } - 15 x$

Find the slope of the curve at the indicated point. -Find an equation of the tangent to the curve $f ( x ) = \sqrt { x + 4 }$ that has slope $\frac { 1 } { 4 }$ .

Find the indicated derivative. - $\frac { d p } { d q }$ if $p = \frac { 1 } { \sqrt { q + 1 } }$

Find the derivative. -w = $\sqrt[3] {z^{6.6}}$ + $5e^{3.1}$

Find the slope of the curve at the indicated point. -Find equations of all tangents to the curve $f ( x ) = \frac { 1 } { x }$ that have slope $- 1$ .

Find the second derivative. - $y = 2 x ^ { 3 } - 7 x ^ { 2 } + 3$

Find the derivative. - $w = z ^ { 6 - e }$

Given the graph of f, find any values of x at which f ' is not defined. -

The graph of a function is given. Choose the answer that represents the graph of its derivative -

Find the derivative of the function. - $r = \frac { \sqrt { \theta } - 8 } { \sqrt { \theta } + 8 }$

Suppose u and v are differentiable functions of x. Use the given values of the functions and their derivatives to find the value of the indicated derivative. - u(2)=6,(2)=2,v(2)=-2,(2)=-5. (2u-4v) at x=2

Find the second derivative. - $y = 9 x ^ { 2 } + 3 x - 7$

Find the derivative of the function. - $z = 6 x ^ { 2 } e ^ { x }$

Provide an appropriate response. - $\text { Does the graph of } \mathrm { f } ( \mathrm { x } ) = \left\{ \begin{array} { l l } 1 , & \mathrm { x } < 0 \\0 , & x = 0 \\- 1 , & x > 0\end{array} \right. \text { have a vertical tangent at the origin? Give reasons for your answer. }$

Functions

Limits and Derivatives

Applications of Derivatives

Integration

Applications of Definite Integrals

Integrals and Transcendental Functions

Techniques of Integration

First-Order Differential Equations

Infinite Sequences and Series

Filters

Exam 3: Differentiation

Find the second derivative of the function. - r=(1+8θ8θ)(8−θ)r = \left( \frac { 1 + 8 \theta } { 8 \theta } \right) ( 8 - \theta )r=(8θ1+8θ​)(8−θ)

Find y'. - y=(6x+x)(6x−x)y = \left( \frac { 6 } { x } + x \right) \left( \frac { 6 } { x } - x \right)y=(x6​+x)(x6​−x)

Find the slope of the curve at the indicated point. -Find the points where the graph of the function have horizontal tangents. f(x)=x3−15xf ( x ) = x ^ { 3 } - 15 xf(x)=x3−15x

Find the slope of the curve at the indicated point. -Find an equation of the tangent to the curve f(x)=x+4f ( x ) = \sqrt { x + 4 }f(x)=x+4​ that has slope 14\frac { 1 } { 4 }41​ .

Find the indicated derivative. - dpdq\frac { d p } { d q }dqdp​ if p=1q+1p = \frac { 1 } { \sqrt { q + 1 } }p=q+1​1​

Find the derivative. -w = z6.63\sqrt[3] {z^{6.6}}3z6.6​ + 5e3.15e^{3.1}5e3.1

Find the slope of the curve at the indicated point. -Find equations of all tangents to the curve f(x)=1xf ( x ) = \frac { 1 } { x }f(x)=x1​ that have slope −1- 1−1 .

Find the second derivative. - y=2x3−7x2+3y = 2 x ^ { 3 } - 7 x ^ { 2 } + 3y=2x3−7x2+3

Find the derivative. - w=z6−ew = z ^ { 6 - e }w=z6−e