Exam 3: Differentiation
Exam 1: Functions124 Questions
Exam 2: Limits and Derivatives213 Questions
Exam 3: Differentiation183 Questions
Exam 4: Applications of Derivatives159 Questions
Exam 5: Integration107 Questions
Exam 6: Applications of Definite Integrals115 Questions
Exam 7: Integrals and Transcendental Functions114 Questions
Exam 8: Techniques of Integration124 Questions
Exam 9: First-Order Differential Equations75 Questions
Exam 10: Infinite Sequences and Series155 Questions
Select questions type
Find the slope of the curve at the indicated point.
-Assume that a watermelon dropped from a tall building falls in sec. Find the watermelon's average speed during the first of fall and the speed at the instant .
(Multiple Choice)
4.7/5  (31)
(31)
Provide an appropriate response.
-Evaluate by first converting it to a derivative at a particular -value.
(Multiple Choice)
4.7/5  (38)
(38)
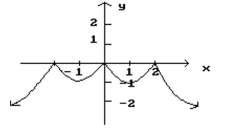
Given the graph of f, find any values of x at which f ' is not defined.
-
(Multiple Choice)
4.8/5  (35)
(35)
Provide an appropriate response.
-Find an equation for the tangent to the curve at the point .
(Multiple Choice)
4.9/5  (44)
(44)
Differentiate the function and find the slope of the tangent line at the given value of the independent variable.
-
(Multiple Choice)
4.7/5  (36)
(36)
The graph of a function is given. Choose the answer that represents the graph of its derivative
-
(Multiple Choice)
4.9/5  (36)
(36)
Showing 61 - 80 of 183
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)