Exam 3: Differentiation
Exam 1: Functions124 Questions
Exam 2: Limits and Derivatives213 Questions
Exam 3: Differentiation183 Questions
Exam 4: Applications of Derivatives159 Questions
Exam 5: Integration107 Questions
Exam 6: Applications of Definite Integrals115 Questions
Exam 7: Integrals and Transcendental Functions114 Questions
Exam 8: Techniques of Integration124 Questions
Exam 9: First-Order Differential Equations75 Questions
Exam 10: Infinite Sequences and Series155 Questions
Select questions type
Calculate the derivative of the function. Then find the value of the derivative as specified.
-
(Multiple Choice)
4.9/5  (39)
(39)
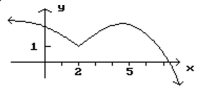
Given the graph of f, find any values of x at which f ' is not defined.
-
(Multiple Choice)
4.7/5  (30)
(30)
The figure shows the graph of a function. At the given value of x, does the function appear to be differentiable, continuous but not differentiable, or neither continuous nor differentiable?
-
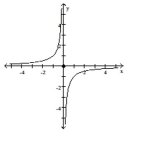
(Multiple Choice)
4.9/5  (28)
(28)
The figure shows the graph of a function. At the given value of x, does the function appear to be differentiable, continuous but not differentiable, or neither continuous nor differentiable?
-
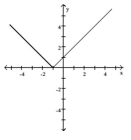
(Multiple Choice)
4.9/5  (37)
(37)
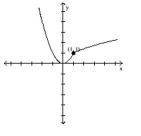
Compare the right-hand and left-hand derivatives to determine whether or not the function is differentiable at the point whose coordinates are given.
-
(Multiple Choice)
4.8/5  (40)
(40)
Provide an appropriate response.
-Can a tangent line to a graph intersect the graph at more than one point? If not, why not. If so, give an example.
(Essay)
4.7/5  (40)
(40)
Provide an appropriate response.
-A heat engine is a device that converts thermal energy into other forms. The thermal efficiency, e, of a heat engin defined by
where is the heat absorbed in one cycle and , the heat released into a reservoir in one cycle, is a constant.
Find .
(Multiple Choice)
5.0/5  (35)
(35)
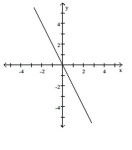
The figure shows the graph of a function. At the given value of x, does the function appear to be differentiable, continuous but not differentiable, or neither continuous nor differentiable?
-
(Multiple Choice)
4.7/5  (37)
(37)
Determine if the piecewise defined function is differentiable at the origin.
-
(Multiple Choice)
4.8/5  (35)
(35)
Showing 161 - 180 of 183
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)