Exam 3: Differentiation
Exam 1: Functions124 Questions
Exam 2: Limits and Derivatives213 Questions
Exam 3: Differentiation183 Questions
Exam 4: Applications of Derivatives159 Questions
Exam 5: Integration107 Questions
Exam 6: Applications of Definite Integrals115 Questions
Exam 7: Integrals and Transcendental Functions114 Questions
Exam 8: Techniques of Integration124 Questions
Exam 9: First-Order Differential Equations75 Questions
Exam 10: Infinite Sequences and Series155 Questions
Select questions type
Find the slope of the curve at the indicated point.
-The power (in ) generated by a particular windmill is given by where is the velocity of the wind (in mph). Find the instantaneous rate of change of power with respect to velocity when the velocity is .
(Multiple Choice)
4.9/5  (30)
(30)
Provide an appropriate response.
-Find the slope of the tangent to the curve at the point where .
(Multiple Choice)
4.9/5  (42)
(42)
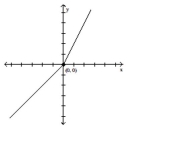
Compare the right-hand and left-hand derivatives to determine whether or not the function is differentiable at the point whose coordinates are given.
-
(Multiple Choice)
4.7/5  (35)
(35)
Suppose u and v are differentiable functions of x. Use the given values of the functions and their derivatives to find the value of the indicated derivative.
- u(1)=5,(1)=-7,v(1)=6,(1)=-3 (2u-4v) at x=1
(Multiple Choice)
4.8/5  (39)
(39)
Differentiate the function and find the slope of the tangent line at the given value of the independent variable.
-
(Multiple Choice)
4.9/5  (30)
(30)
Provide an appropriate response.
-Find all points on the graph of with tangent lines perpendicular to the line .
(Multiple Choice)
4.9/5  (33)
(33)
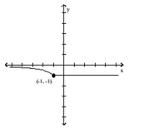
Compare the right-hand and left-hand derivatives to determine whether or not the function is differentiable at the point whose coordinates are given.
-
(Multiple Choice)
4.7/5  (38)
(38)
Calculate the derivative of the function. Then find the value of the derivative as specified.
-
(Multiple Choice)
4.8/5  (42)
(42)
Showing 121 - 140 of 183
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)