Exam 1: Functions and Models
Exam 1: Functions and Models179 Questions
Exam 2: Limits and Derivatives139 Questions
Exam 3: Differentiation Rules160 Questions
Exam 4: Applications of Differentiation160 Questions
Exam 5: Integrals158 Questions
Exam 6: Applications of Integration157 Questions
Exam 7: Techniques of Integration160 Questions
Exam 8: Further Applications of Integration160 Questions
Exam 9: Differential Equations160 Questions
Exam 10: Parametric Equations and Polar Coordinates160 Questions
Exam 11: Infinite Sequences and Series159 Questions
Exam 12: Vectors and the Geometry of Space160 Questions
Exam 13: Vector Functions159 Questions
Exam 14: Partial Derivatives158 Questions
Exam 15: Multiple Integrals159 Questions
Exam 16: Vector Calculus159 Questions
Exam 17: Second-Order Differential Equations159 Questions
Select questions type
Suppose the distance (in feet) covered by a car moving along a straight road after sec is given by the function . Calculate the (instantaneous) velocity of the car when .
Select the correct answer.
(Multiple Choice)
4.8/5  (31)
(31)
Graph the function by hand, not by plotting points, but by starting with the graph of one of the standard functions and then applying the appropriate transformations.
Select the correct answer.
(Multiple Choice)
4.9/5  (28)
(28)
The graph of the function has been stretched horizontally by a factor of 2 . Find the function for the transformed graph.
(Multiple Choice)
4.8/5  (32)
(32)
Scientists have discovered that a linear relationship exists between the amount of flobberworm mucus secretions and the air temperature. When the temperature is , the flobberworms each secrete 16 grams of mucus a day; when the temperature is , they each secrete 22 grams of mucus a day. Find a function that gives the amount of mucus secreted on a given day, where is the temperature of that day in degrees Fahrenheit.
(Multiple Choice)
4.7/5  (36)
(36)
Use the graph of the function to state the value of , if it exists.
(Short Answer)
5.0/5  (34)
(34)
The curve with the equation is called an asteroid. Find an equation of the tangent to the curve at the point .
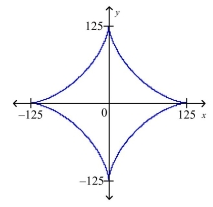
(Short Answer)
4.9/5  (31)
(31)
Suppose that the graph of is given is given. Describe how the graph of the function can be obtained from the graph of .
(Multiple Choice)
4.9/5  (29)
(29)
By graphing the function
and zooming in toward the point where the graph crosses the -axis, estimate the value of .
(Short Answer)
4.8/5  (27)
(27)
Graph the function by hand, not by plotting points, but by starting with the graph of one of the standard functions and then applying the appropriate transformations.
(Essay)
4.9/5  (38)
(38)
The monthly cost of driving a car depends on the number of miles driven. Julia found that in October it cost her to drive and in July it cost her to drive . Express the monthly cost as a function of the distance driven assuming that a linear relationship gives a suitable model.
(Short Answer)
4.9/5  (41)
(41)
Showing 141 - 160 of 179
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)