Exam 1: Functions and Models
Exam 1: Functions and Models179 Questions
Exam 2: Limits and Derivatives139 Questions
Exam 3: Differentiation Rules160 Questions
Exam 4: Applications of Differentiation160 Questions
Exam 5: Integrals158 Questions
Exam 6: Applications of Integration157 Questions
Exam 7: Techniques of Integration160 Questions
Exam 8: Further Applications of Integration160 Questions
Exam 9: Differential Equations160 Questions
Exam 10: Parametric Equations and Polar Coordinates160 Questions
Exam 11: Infinite Sequences and Series159 Questions
Exam 12: Vectors and the Geometry of Space160 Questions
Exam 13: Vector Functions159 Questions
Exam 14: Partial Derivatives158 Questions
Exam 15: Multiple Integrals159 Questions
Exam 16: Vector Calculus159 Questions
Exam 17: Second-Order Differential Equations159 Questions
Select questions type
Use the graph of the function to state the value of , if it exists.
(Short Answer)
4.9/5  (33)
(33)
Evaluate the function
at the given numbers (correct to six decimal places). Use the results to guess the value of the limit .
x f(x) 1.6 1.8 1.9 1.99 1.999 2.4 2.2 2.1 2.01 2.001 Limit
(Short Answer)
4.9/5  (41)
(41)
Consider the following function.
Determine the values of for which exists.
(Short Answer)
4.8/5  (37)
(37)
You are given and a tolerance . Find a number such that whenever .
(Short Answer)
4.7/5  (28)
(28)
Is there a number such that exists? If so, find the value of and the value of the limit.
(Short Answer)
4.8/5  (36)
(36)
Find the numbers, if any, where the function is discontinuous.
(Multiple Choice)
4.7/5  (36)
(36)
The point lies on the curve . If is the point , use your calculator to find the slope of the secant line (correct to six decimal places) for the value .
(Multiple Choice)
4.9/5  (31)
(31)
The volume of a right circular cone of radius and height is . Suppose that the radius and height of the cone are changing with respect to time .
a. Find a relationship between , and .
b. At a certain instant of time, the radius and height of the cone are 12 in. and 13 in. and are increasing at the rate of and , respectively. How fast is the volume of the cone increasing?
(Short Answer)
4.8/5  (29)
(29)
Two curves are said to be orthogonal if their tangent lines are perpendicular at each point of intersection of the curves. Show that the curves of the given equations are orthogonal.
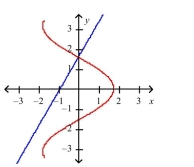
(Short Answer)
4.8/5  (45)
(45)
Showing 21 - 40 of 179
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)