Exam 3: Differentiation Rules
Exam 1: Functions and Models179 Questions
Exam 2: Limits and Derivatives139 Questions
Exam 3: Differentiation Rules160 Questions
Exam 4: Applications of Differentiation160 Questions
Exam 5: Integrals158 Questions
Exam 6: Applications of Integration157 Questions
Exam 7: Techniques of Integration160 Questions
Exam 8: Further Applications of Integration160 Questions
Exam 9: Differential Equations160 Questions
Exam 10: Parametric Equations and Polar Coordinates160 Questions
Exam 11: Infinite Sequences and Series159 Questions
Exam 12: Vectors and the Geometry of Space160 Questions
Exam 13: Vector Functions159 Questions
Exam 14: Partial Derivatives158 Questions
Exam 15: Multiple Integrals159 Questions
Exam 16: Vector Calculus159 Questions
Exam 17: Second-Order Differential Equations159 Questions
Select questions type
Find the dimensions of the rectangle of largest area that can be inscribed in an equilateral triangle of side if one side of the rectangle lies on the base of the triangle.
Round your answer to the nearest tenth.
(Short Answer)
5.0/5  (43)
(43)
Find the dimensions of a rectangle of area that has the smallest possible perimeter.
(Multiple Choice)
4.9/5  (41)
(41)
Given that the graph of passes through the point and that the slope of its tangent line at is , find . Select the correct answer.
(Multiple Choice)
4.8/5  (41)
(41)
Given .
(a) Find the intervals on which is increasing or decreasing.
(b) Find the relative maxima and relative minima of .
(Multiple Choice)
4.8/5  (39)
(39)
Find two positive numbers whose product is 196 and whose sum is a minimum.
(Multiple Choice)
5.0/5  (41)
(41)
Determine where the graph of is concave upward and where it is concave downward. Also, find all inflection points of the function.
(Short Answer)
4.8/5  (30)
(30)
At 4:00 P.M. a car's speedometer reads . At 4:15 it reads . At some time between and the acceleration is exactly . Find .
(Short Answer)
4.8/5  (36)
(36)
A woman at a point on the shore of a circular lake with radius wants to arrive at the point diametrically opposite on the other side of the lake in the shortest possible time. She can walk at the rate of and row a boat at . How should she proceed? (Find ). Round the result, if necessary, to the nearest hundredth.
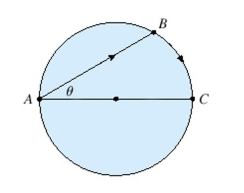
(Multiple Choice)
4.9/5  (42)
(42)
A manufacturer has been selling 1,200 television sets a week at each. A market survey indicates that for each rebate offered to the buyer, the number of sets sold will increase by 60 per week. Find the demand function.
(Short Answer)
4.9/5  (34)
(34)
The graph of the derivative of a continuous function is shown. On what intervals is decreasing?
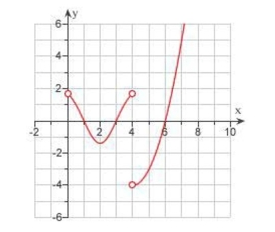 .
.
(Short Answer)
4.8/5  (34)
(34)
The average cost of producing units of a commodity is given by the equation
Find the marginal cost at a production level of 1,255 units.
(Short Answer)
4.9/5  (43)
(43)
Showing 61 - 80 of 160
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)