Exam 3: Differentiation Rules
Exam 1: Functions and Models179 Questions
Exam 2: Limits and Derivatives139 Questions
Exam 3: Differentiation Rules160 Questions
Exam 4: Applications of Differentiation160 Questions
Exam 5: Integrals158 Questions
Exam 6: Applications of Integration157 Questions
Exam 7: Techniques of Integration160 Questions
Exam 8: Further Applications of Integration160 Questions
Exam 9: Differential Equations160 Questions
Exam 10: Parametric Equations and Polar Coordinates160 Questions
Exam 11: Infinite Sequences and Series159 Questions
Exam 12: Vectors and the Geometry of Space160 Questions
Exam 13: Vector Functions159 Questions
Exam 14: Partial Derivatives158 Questions
Exam 15: Multiple Integrals159 Questions
Exam 16: Vector Calculus159 Questions
Exam 17: Second-Order Differential Equations159 Questions
Select questions type
A production editor decided that a promotional flyer should have a 1 -in. margin at the top and the bottom, and a -in. margin on each side. The editor further stipulated that the flyer should have an area of . Determine the dimensions of the flyer that will result in the maximum printed area on the flyer.
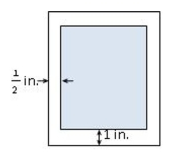
(Multiple Choice)
4.8/5  (44)
(44)
An aircraft manufacturer wants to determine the best selling price for a new airplane. The company estimates that the initial cost of designing the airplane and setting up the factories in which to build it will be 700 million dollars. The additional cost of manufacturing each plane can be modeled by the function
where is the number of aircraft produced and is the manufacturing cost, in millions of dollars. The company estimates that if it charges a price (in millions of dollars) for each plane, it will be able to sell
Find the cost function.
(Short Answer)
4.9/5  (39)
(39)
Verify that the function satisfies the three hypotheses of Rolle's Theorem on the given interval. Then find all numbers that satisfy the conclusion of Rolle's Theorem.
(Short Answer)
4.8/5  (33)
(33)
For what values of and is is an inflection point of the curve ? What additional inflection points does the curve have?
(Short Answer)
4.7/5  (42)
(42)
The size of the monthly repayment that amortizes a loan of dollars in years at an interest rate of per year, compounded monthly, on the unpaid balance is given by
The value of can be found by performing the iteration
A family secured a loan of from a bank to finance the purchase of a house. They have agreed to repay the loan in equal monthly installments of over 25 years. Find the interest rate on this loan. Round the rate to one decimal place.
(Short Answer)
4.9/5  (40)
(40)
Find the dimensions of the rectangle of largest area that can be inscribed in an equilateral triangle of side if one side of the rectangle lies on the base of the triangle.
Round your answer to the nearest tenth.
(Short Answer)
4.9/5  (41)
(41)
Estimate the value of by using three iterations of Newton's method to solve the equation with initial estimate . Round your final estimate to four decimal places. Select the correct answer.
(Multiple Choice)
4.9/5  (33)
(33)
The size of the monthly repayment that amortizes a loan of dollars in years at an interest rate of per year, compounded monthly, on the unpaid balance is given by
The value of can be found by performing the iteration
A family secured a loan of from a bank to finance the purchase of a house. They have agreed to repay the loan in equal monthly installments of over 25 years. Find the interest rate on this loan. Round the rate to one decimal place.
(Short Answer)
4.9/5  (33)
(33)
A production editor decided that a promotional flyer should have a 1 -in. margin at the top and the bottom, and a -in. margin on each side. The editor further stipulated that the flyer should have an area of 72 in. . Determine the dimensions of the flyer that will result in the maximum printed area on the flyer.
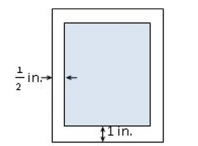
(Short Answer)
4.8/5  (39)
(39)
Use the Second Derivative Test to find the relative extrema, if any, of the function
(Multiple Choice)
4.9/5  (28)
(28)
Showing 101 - 120 of 160
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)