Exam 8: Further Applications of Integration
Exam 1: Functions and Models179 Questions
Exam 2: Limits and Derivatives139 Questions
Exam 3: Differentiation Rules160 Questions
Exam 4: Applications of Differentiation160 Questions
Exam 5: Integrals158 Questions
Exam 6: Applications of Integration157 Questions
Exam 7: Techniques of Integration160 Questions
Exam 8: Further Applications of Integration160 Questions
Exam 9: Differential Equations160 Questions
Exam 10: Parametric Equations and Polar Coordinates160 Questions
Exam 11: Infinite Sequences and Series159 Questions
Exam 12: Vectors and the Geometry of Space160 Questions
Exam 13: Vector Functions159 Questions
Exam 14: Partial Derivatives158 Questions
Exam 15: Multiple Integrals159 Questions
Exam 16: Vector Calculus159 Questions
Exam 17: Second-Order Differential Equations159 Questions
Select questions type
Find the centroid of the region bounded by the given curves. Select the correct answer.
(Multiple Choice)
4.7/5  (37)
(37)
For the following exercise, (a) plot the graph of the function , (b) write an integral giving the arc length of the graph of the function over the indicated interval, and (c) find the arc length of the curve accurate to two decimal places.
(Short Answer)
4.9/5  (33)
(33)
Find the area of the surface obtained by rotating the circle about the line .
(Multiple Choice)
4.8/5  (45)
(45)
You are given the shape of the vertical ends of a trough that is completely filled with water. Find the force exerted by the water on one end of the trough. (The weight density of water is .)
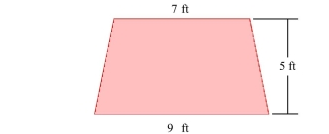
(Short Answer)
4.9/5  (33)
(33)
Find the arc length of the graph of the given equation on the specified interval.
(Multiple Choice)
5.0/5  (31)
(31)
An aquarium is long, wide, and deep. If the aquarium is filled with water, find the force exerted by the water (a) on the bottom of the aquarium, (b) on the longer side of the aquarium, and (c) on the shorter side of the aquarium. (The weight density of water is .)
(Short Answer)
4.8/5  (41)
(41)
Find the center of mass of the lamina of the region shown if the density of the circular lamina is six times that of the rectangular lamina.
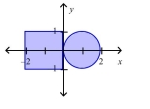
(Short Answer)
4.7/5  (31)
(31)
Find the area of the surface obtained by revolving the given curve about the -axis.
(Short Answer)
4.8/5  (35)
(35)
Write an integral giving the area of the surface obtained by revolving the curve about the -axis. (Do not evaluate the integral.)
(Multiple Choice)
4.8/5  (32)
(32)
A vertical plate is submerged in water (the surface of the water coincides with the -axis). Find the force exerted by the water on the plate. (The weight density of water is .)
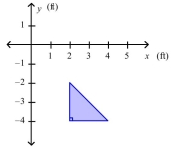
(Short Answer)
4.8/5  (33)
(33)
Find the centroid of the region bounded by the graphs of the given equations.
(Multiple Choice)
4.8/5  (41)
(41)
Find the centroid of the region bounded by the graphs of the given equations.
(Short Answer)
4.8/5  (34)
(34)
Dye dilution is a method of measuring cardiac output. If of dye is used and is the concentration of the dye at time , then the cardiac output over the time interval is given by
Find the cardiac output over the time interval if the dye dilution method is used with of dye and the dye concentration, in , is modeled by
where is measured in seconds.
(Multiple Choice)
4.8/5  (37)
(37)
The marginal revenue from producing units of a certain product is
(in dollars per unit).
Find the increase in revenue if the production level is raised from 1,100 units to 1,700 units.
(Multiple Choice)
4.7/5  (30)
(30)
You are given the shape of the vertical ends of a trough that is completely filled with water. Find the force exerted by the water on one end of the trough. (The weight density of water is .)
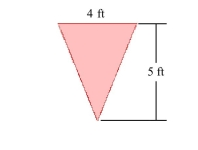
(Short Answer)
4.8/5  (54)
(54)
Find the centroid of the region bounded by the given curves.
(Multiple Choice)
4.8/5  (35)
(35)
Set up, but do not evaluate, an integral for the length of the curve.
(Short Answer)
4.9/5  (40)
(40)
The standard deviation for a random variable with probability density function and mean is defined
Find the standard deviation for an exponential density function with mean
(Multiple Choice)
4.7/5  (35)
(35)
Showing 61 - 80 of 160
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)