Exam 11: Derivatives of Exponential and Logarithmic Functions
Exam 1: Fundamental Concepts of Algebra119 Questions
Exam 2: Equations and Inequalities94 Questions
Exam 3: Functions and Graphs96 Questions
Exam 4: Polynomial and Rational Functions105 Questions
Exam 5: Exponential and Logarithmic Functions94 Questions
Exam 6: Systems of Equations and Inequalities96 Questions
Exam 7: Matrices and Determinants94 Questions
Exam 8: Limits and Derivatives77 Questions
Exam 9: Applications of the Derivative83 Questions
Exam 10: Further Applications of the Derivative83 Questions
Exam 11: Derivatives of Exponential and Logarithmic Functions121 Questions
Exam 12: Integration and Its Applications74 Questions
Exam 13: Techniques of Integration50 Questions
Exam 14: Functions of Several Variables92 Questions
Exam 15: Trigonometric Functions Web60 Questions
Exam 16: Series and Taylor Polynomials Web127 Questions
Exam 17: Probability Web89 Questions
Select questions type
What percent of a present amount of radioactive radium will remain after 900 years?
(Multiple Choice)
4.7/5  (40)
(40)
How long (in years) would $450 have to be invested at an annual rate of 12%, compounded continuously, to amount to $790?
(Multiple Choice)
4.8/5  (26)
(26)
Solve the exponential equation. Give the answer correct to 3 decimal places.
(Multiple Choice)
4.9/5  (37)
(37)
Use the properties of logarithms to approximate given that and
(Multiple Choice)
4.9/5  (33)
(33)
What is the annual percentage yield (or effective annual rate) for a nominal rate of 9% compounded quarterly?
(Multiple Choice)
4.7/5  (40)
(40)
The demand function for a product is modeled by . What is the limit of the price as x increases without bound? Round your answer to two decimal places where applicable.
(Multiple Choice)
4.8/5  (34)
(34)
Find the exponential function y=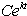 that passes through the two given points and .
that passes through the two given points and .
(Multiple Choice)
4.8/5  (38)
(38)
Use the properties of logarithms to write the expression as a sum, difference, or multiple of logarithms.
(Multiple Choice)
4.9/5  (41)
(41)
The relationship between the number of decibels and the intensity of a sound I in watts per square centimeter is given by . Find the rate of change in the number of decibels when the intensity is watt per square centimeter. Round your answer to the nearest decibel.
(Multiple Choice)
4.7/5  (36)
(36)
The number of a certain type of bacteria increases continuously at a rate proportional to the number present. There are 100 present initially, and 200 present 7 hours later. How many will there be 20 hours after the initial time? Round your answer to the nearest integer.
(Multiple Choice)
4.8/5  (34)
(34)
Suppose that the annual rate of inflation averages 4% over the next 10 years. With this rate of inflation, the approximate cost C of goods or services during any year in that decade will be given by C(t) = P(1.04)t, 0 10 where t is time in years and P is the present cost. If the price of an oil change for your car is presently 24.95, estimate the price 9 years from now. Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (30)
(30)
Showing 21 - 40 of 121
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)