Exam 9: Applications of the Derivative
Exam 1: Fundamental Concepts of Algebra119 Questions
Exam 2: Equations and Inequalities94 Questions
Exam 3: Functions and Graphs96 Questions
Exam 4: Polynomial and Rational Functions105 Questions
Exam 5: Exponential and Logarithmic Functions94 Questions
Exam 6: Systems of Equations and Inequalities96 Questions
Exam 7: Matrices and Determinants94 Questions
Exam 8: Limits and Derivatives77 Questions
Exam 9: Applications of the Derivative83 Questions
Exam 10: Further Applications of the Derivative83 Questions
Exam 11: Derivatives of Exponential and Logarithmic Functions121 Questions
Exam 12: Integration and Its Applications74 Questions
Exam 13: Techniques of Integration50 Questions
Exam 14: Functions of Several Variables92 Questions
Exam 15: Trigonometric Functions Web60 Questions
Exam 16: Series and Taylor Polynomials Web127 Questions
Exam 17: Probability Web89 Questions
Select questions type
A point is moving along the graph of the function such that centimeters per second. Find dy/dt for the given values of x. (a) (b)
(Multiple Choice)
4.8/5  (30)
(30)
Profit. Suppose that the monthly revenue and cost (in dollars) for x units of a product are At what rate per month is the profit changing if the number of units produced and sold is 100 and is increasing at a rate of 10 units per month?
(Multiple Choice)
4.8/5  (44)
(44)
Find for the equation by implicit differentiation and evaluate the derivative at the point .
(Multiple Choice)
4.8/5  (30)
(30)
The graph of f is shown in the figure. Sketch a graph of the derivative of f. 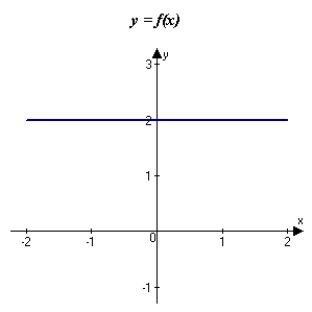
(Multiple Choice)
4.8/5  (32)
(32)
A brick becomes dislodged from the Empire State Building (at a height of 1175 feet) and falls to the sidewalk below. Write the position s(t), velocity v(t), and acceleration a(t) as functions of time.
(Multiple Choice)
4.8/5  (35)
(35)
Approximate the critical numbers of the function shown in the graph and determine whether the function has a relative maximum, a relative minimum, an absolute maximum, an absolute minimum, or none of these at each critical number on the interval shown. 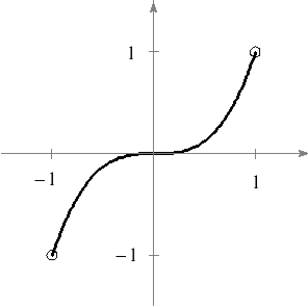
(Multiple Choice)
4.8/5  (42)
(42)
The lengths of the edges of a cube are increasing at a rate of 7 ft/min. At what rate is the surface area changing when the edges are 22 ft long?
(Multiple Choice)
4.9/5  (32)
(32)
A baseball diamond has the shape of a square with sides 90 feet long (see figure). A player running from second base to third base at a speed of 26 feet per second is 80 feet from third base. At what rate is the player's distance s from home plate changing? Round your answer to one decimal place. 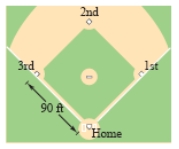
(Multiple Choice)
4.8/5  (34)
(34)
Assume that x and y are differentiable functions of t. Find dx/dt given that , , and
(Multiple Choice)
4.9/5  (34)
(34)
Volume and radius. Suppose that air is being pumped into a spherical balloon at a rate of At what rate is the radius of the balloon increasing when the radius is 3 in.?
(Multiple Choice)
4.8/5  (29)
(29)
Find implicitly and explicitly(the explicit functions are shown on the graph) and show that the results are equivalent. Use the graph to estimate the slope of the tangent line at the labeled point. Then verify your result analytically by evaluating at the point. 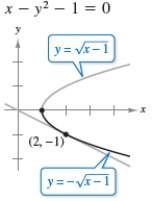
(Multiple Choice)
4.8/5  (48)
(48)
Identify the open intervals where the function is increasing or decreasing.
(Multiple Choice)
4.9/5  (36)
(36)
Find the second derivative for the function and solve the equation .
(Multiple Choice)
4.7/5  (40)
(40)
Showing 21 - 40 of 83
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)