Exam 9: Applications of the Derivative
Exam 1: Fundamental Concepts of Algebra119 Questions
Exam 2: Equations and Inequalities94 Questions
Exam 3: Functions and Graphs96 Questions
Exam 4: Polynomial and Rational Functions105 Questions
Exam 5: Exponential and Logarithmic Functions94 Questions
Exam 6: Systems of Equations and Inequalities96 Questions
Exam 7: Matrices and Determinants94 Questions
Exam 8: Limits and Derivatives77 Questions
Exam 9: Applications of the Derivative83 Questions
Exam 10: Further Applications of the Derivative83 Questions
Exam 11: Derivatives of Exponential and Logarithmic Functions121 Questions
Exam 12: Integration and Its Applications74 Questions
Exam 13: Techniques of Integration50 Questions
Exam 14: Functions of Several Variables92 Questions
Exam 15: Trigonometric Functions Web60 Questions
Exam 16: Series and Taylor Polynomials Web127 Questions
Exam 17: Probability Web89 Questions
Select questions type
The radius r of a sphere is increasing at a rate of 3 inches per minute. Find the rate of change of volume when r = 17 inches. Round your answer to one decimal place.
(Multiple Choice)
4.7/5  (29)
(29)
Boat docking. Suppose that a boat is being pulled toward a dock by a winch that is 24 ft above the level of the boat deck. If the winch is pulling the cable at a rate of 23 ft/min, at what rate is the boat approaching the dock when it is 32 ft from the dock? Use the figure below. 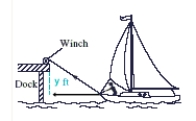
(Multiple Choice)
4.8/5  (39)
(39)
Find the second derivative for the function and solve the equation .
(Multiple Choice)
4.9/5  (39)
(39)
A point is moving along the graph of the function such that centimeters per second. Find dy/dt when .
(Multiple Choice)
4.8/5  (30)
(30)
Determine whether the statement is true or false. If it is false, explain why or give an example that shows it is false. If
(Multiple Choice)
4.8/5  (30)
(30)
The graph of f is shown. Graph f, f' and f'' on the same set of coordinate axes. 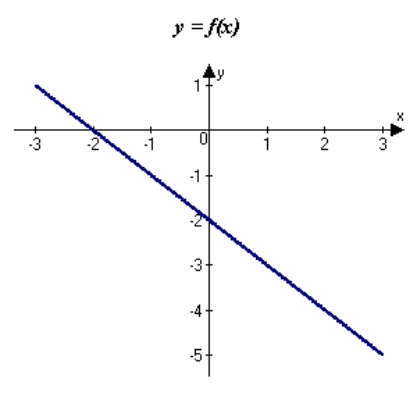
(Multiple Choice)
4.7/5  (28)
(28)
A fast-food restaurant determines the cost model, and revenue model, for where x is the number of hamburgers sold. Determine the intervals on which the profit function is increasing and on which it is decreasing.
(Multiple Choice)
4.7/5  (32)
(32)
Determine the open intervals on which the graph of is concave downward or concave upward.
(Multiple Choice)
4.9/5  (30)
(30)
The graph of f is shown in the figure. Sketch a graph of the derivative of f. 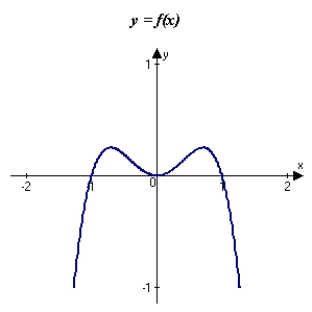
(Multiple Choice)
4.7/5  (29)
(29)
The number of people who donated to a certain organization between 1975 and 1992 can be modeled by the equation donors, where t is the number of years after 1975. Find the inflection point(s) from through , if any exist.
(Multiple Choice)
4.8/5  (28)
(28)
For the function : (a) Find the critical numbers of f (if any);
(b) Find the open intervals where the function is increasing or decreasing; and
(c) Apply the First Derivative Test to identify all relative extrema.
Then use a graphing utility to confirm your results.
(Multiple Choice)
4.9/5  (27)
(27)
Suppose the resident population P(in millions) of the United States can be modeled by , where corresponds to 1800. Analytically find the minimum and maximum populations in the U.S. for .
(Multiple Choice)
4.9/5  (32)
(32)
Identify the open intervals where the function is increasing or decreasing.
(Multiple Choice)
4.9/5  (38)
(38)
An airplane flying at an altitude of 5 miles passes directly over a radar antenna. When the airplane is 50 miles away (s = 50), the radar detects that the distance s is changing at a rate of 280 miles per hour. What is the speed of the airplane? Round your answer to the nearest integer.
(Multiple Choice)
4.8/5  (27)
(27)
The graph of f is shown in the figure. Sketch a graph of the derivative of f. 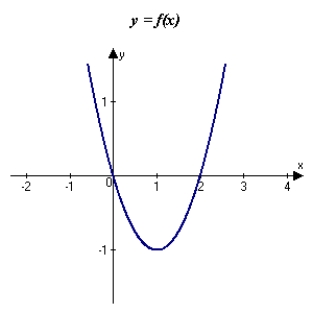
(Multiple Choice)
4.9/5  (43)
(43)
Find all relative extrema of the function . Use the Second Derivative Test where applicable.
(Multiple Choice)
4.7/5  (31)
(31)
Showing 61 - 80 of 83
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)