Exam 4: Polynomial and Rational Functions
Exam 1: Fundamental Concepts of Algebra119 Questions
Exam 2: Equations and Inequalities94 Questions
Exam 3: Functions and Graphs96 Questions
Exam 4: Polynomial and Rational Functions105 Questions
Exam 5: Exponential and Logarithmic Functions94 Questions
Exam 6: Systems of Equations and Inequalities96 Questions
Exam 7: Matrices and Determinants94 Questions
Exam 8: Limits and Derivatives77 Questions
Exam 9: Applications of the Derivative83 Questions
Exam 10: Further Applications of the Derivative83 Questions
Exam 11: Derivatives of Exponential and Logarithmic Functions121 Questions
Exam 12: Integration and Its Applications74 Questions
Exam 13: Techniques of Integration50 Questions
Exam 14: Functions of Several Variables92 Questions
Exam 15: Trigonometric Functions Web60 Questions
Exam 16: Series and Taylor Polynomials Web127 Questions
Exam 17: Probability Web89 Questions
Select questions type
The height in feet of a projectile with an initial velocity of 128 feet per second and an initial height of 50 feet is a function of time t, in seconds, given by Find the maximum height of the projectile.
(Multiple Choice)
4.8/5  (41)
(41)
The rational function models the number of milligrams of medication in the bloodstream of a patient t hours after 150 milligrams of the medication have been injected into the patient's bloodstream. What will M approach as ?
(Multiple Choice)
4.8/5  (42)
(42)
Simplify the rational expression, , by using long division or synthetic division.
(Multiple Choice)
4.8/5  (28)
(28)
Simplify and write the following complex number in standard form.
(Multiple Choice)
4.8/5  (33)
(33)
Find the zeros of the polynomial function below. If a zero is a multiple zero, state its multiplicity.
(Multiple Choice)
5.0/5  (32)
(32)
A company that produces video games estimates that the profit (in dollars) for selling a new game is given by where is the advertising expense (in tens of thousands of dollars). Using this model, how much should the company spend on advertising to obtain a profit of $6,100,000? Round to the nearest dollar.
(Multiple Choice)
4.9/5  (37)
(37)
Given , determine the equations of any slant and vertical asymptote.
(Multiple Choice)
4.7/5  (30)
(30)
The graph of the function is shown below. Determine the domain. 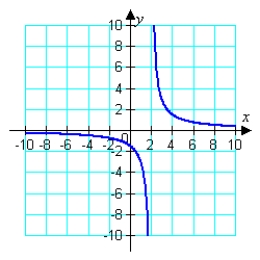
(Multiple Choice)
4.8/5  (29)
(29)
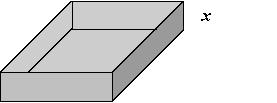
An open box is to be made from a square piece of cardboard, 36 inches on a side, by cutting equal squares with sides of length x from the corners and turning up the sides (see figure below). After determining the function V, in terms of x, that represents the volume of the box, use a graphing utility to estimate the dimensions that will maximize its volume. 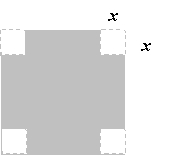
(Multiple Choice)
4.8/5  (37)
(37)
Determine the vertical and slant asymptotes of the rational function below.
(Multiple Choice)
4.8/5  (32)
(32)
The demand and cost equations for a stethoscope are given by
and
where is the unit price (in dollars), is the total cost (in dollars), and is the number of units. The total profit (in dollars) obtained by producing and selling units is given by Determine a price that would yield a profit of $6.9 million.
(Multiple Choice)
4.9/5  (36)
(36)
Find an equation of the parabola that has a vertex at and whose graph passes through the point
(Multiple Choice)
4.7/5  (37)
(37)
Write the polynomial as the product of linear and quadratic factors that are irreducible over the reals.
(Multiple Choice)
4.8/5  (38)
(38)
The fuel efficiency, in miles per gallon, for a certain midsize car at various speeds, in miles per hour, is given in the table below. 25 20 55 31 30 24 60 33 35 32 65 30 40 35 70 24 45 36 75 22 50 40 Find a quadratic model for these data and use it to predict the fuel efficiency of this car when it is traveling at a speed of 40 mph. Do not round any values in your calculations but round the final answer to the nearest tenth.
(Multiple Choice)
4.9/5  (40)
(40)
Showing 41 - 60 of 105
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)