Exam 3: Functions and Graphs
Exam 1: Fundamental Concepts of Algebra119 Questions
Exam 2: Equations and Inequalities94 Questions
Exam 3: Functions and Graphs96 Questions
Exam 4: Polynomial and Rational Functions105 Questions
Exam 5: Exponential and Logarithmic Functions94 Questions
Exam 6: Systems of Equations and Inequalities96 Questions
Exam 7: Matrices and Determinants94 Questions
Exam 8: Limits and Derivatives77 Questions
Exam 9: Applications of the Derivative83 Questions
Exam 10: Further Applications of the Derivative83 Questions
Exam 11: Derivatives of Exponential and Logarithmic Functions121 Questions
Exam 12: Integration and Its Applications74 Questions
Exam 13: Techniques of Integration50 Questions
Exam 14: Functions of Several Variables92 Questions
Exam 15: Trigonometric Functions Web60 Questions
Exam 16: Series and Taylor Polynomials Web127 Questions
Exam 17: Probability Web89 Questions
Select questions type
Plot the points below whose coordinates are given on a Cartesian coordinate system.
(Multiple Choice)
4.9/5  (38)
(38)
The cost of sending an overnight package from New York to Atlanta is $9.80 for up to, but not including, the first pound and $3.50 for each additional pound (or portion of a pound). A model for the total cost of sending the package is where is the weight of the package (in pounds). Sketch the graph of this function. Note that the function is the greatest integer function.
(Multiple Choice)
4.8/5  (29)
(29)
Describe the sequence of transformations from to . Then sketch the graph of by hand. Verify with a graphing utility.
(Multiple Choice)
4.8/5  (35)
(35)
The point on the graph of has been shifted to the point after a rigid transformation. Identify the shift and write the new function in terms of .
(Multiple Choice)
4.8/5  (41)
(41)
Assuming that the graph shown has y-axis symmetry, sketch the complete graph. 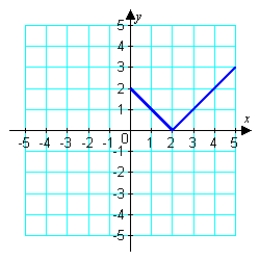
(Multiple Choice)
4.9/5  (30)
(30)
Assume that y is directly proportional to x. If and , determine a linear model that relates y and x.
(Multiple Choice)
4.7/5  (36)
(36)
The weekly profit (in hundreds of dollars) for a business from a product is given by the model where is the amount (in hundreds of dollars) spent on advertising. Rewrite the profit equation so that measures advertising expenditures in dollars.
(Multiple Choice)
4.7/5  (38)
(38)
After completing the table, use the resulting solution points to sketch the graph of the equation . x 0 1 2 3 4 y (x,y) 
(Essay)
4.9/5  (38)
(38)
Graph the following equation by plotting points that satisfy the equation.
(Multiple Choice)
4.8/5  (38)
(38)
Find the midpoint of the line segment joining the points. (0, 9), (4, -3)
(Multiple Choice)
4.9/5  (33)
(33)
Consider the graph of Use your knowledge of rigid and nonrigid transformations to write an equation for the following descriptions. The graph of is shifted four units to the right.
(Multiple Choice)
4.8/5  (26)
(26)
The population (in millions of people) of North America from 1980 to 2050 can be modeled by where represents the year, with corresponding to 2050. Find the y-intercept of the graph of the model. What does it represent in the given situation?
(Multiple Choice)
4.8/5  (40)
(40)
Identify the transformation shown in the graph and identify the associated common function. Write the equation of the graphed function. 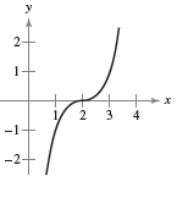
(Multiple Choice)
5.0/5  (28)
(28)
Showing 81 - 96 of 96
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)