Exam 5: Discrete Probability Distributions
Exam 1: Defining and Collecting Data207 Questions
Exam 2: Organizing and Visualizing Variables213 Questions
Exam 3: Numerical Descriptive Measures167 Questions
Exam 4: Basic Probability171 Questions
Exam 5: Discrete Probability Distributions217 Questions
Exam 6: The Normal Distributions and Other Continuous Distributions189 Questions
Exam 7: Sampling Distributions135 Questions
Exam 8: Confidence Interval Estimation189 Questions
Exam 9: Fundamentals of Hypothesis Testing: One-Sample Tests187 Questions
Exam 10: Two-Sample Tests208 Questions
Exam 11: Analysis of Variance216 Questions
Exam 12: Chi-Square and Nonparametric Tests178 Questions
Exam 13: Simple Linear Regression214 Questions
Exam 14: Introduction to Multiple Regression336 Questions
Exam 15: Multiple Regression Model Building99 Questions
Exam 16: Time-Series Forecasting173 Questions
Exam 17: Business Analytics115 Questions
Exam 18: A Roadmap for Analyzing Data329 Questions
Exam 19: Statistical Applications in Quality Management Online162 Questions
Exam 20: Decision Making Online129 Questions
Exam 21: Understanding Statistics: Descriptive and Inferential Techniques39 Questions
Select questions type
The number of power outages at a nuclear power plant has a Poisson distribution with a mean of 6 outages per year.The probability that there will be no more than 1 power outage in a year is ____________.
(Short Answer)
4.7/5  (30)
(30)
SCENARIO 5-8 Two different designs on a new line of winter jackets for the coming winter are available for your manufacturing plants.Your profit (in thousands of dollars)will depend on the taste of the consumers when winter arrives.The probability of the three possible different tastes of the consumers and the corresponding profits are presented in the following table. 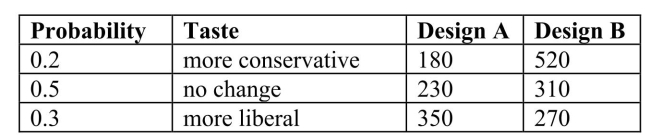 -Referring to Scenario 5-8, what is your expected profit when Design B is chosen?
-Referring to Scenario 5-8, what is your expected profit when Design B is chosen?
(Short Answer)
4.7/5  (31)
(31)
SCENARIO 5-9 A major hotel chain keeps a record of the number of mishandled bags per 1,000 customers.In a recent year, the hotel chain had 4.06 mishandled bags per 1,000 customers.Assume that the number of mishandled bags has a Poisson distribution.
-Referring to Scenario 5-9, what is the probability that in the next 1,000 customers, the hotel chain will have no more than two and at least eight mishandled bags?
(Short Answer)
4.8/5  (34)
(34)
Current estimates suggest that 75% of the home-based computers in a foreign country have access to on-line services.Suppose 20 people with home-based computers were randomly and independently sampled.Find the probability that fewer than 10 of those sampled currently have access to on-line services.
(Short Answer)
4.9/5  (38)
(38)
The number of 911 calls in a small city has a Poisson distribution with a mean of 10 calls a day.The probability of seven 911 calls in a day is ____________.
(Short Answer)
4.8/5  (29)
(29)
If remains constant in a binomial distribution, an increase in n will not change the mean.
(True/False)
4.8/5  (29)
(29)
SCENARIO 5-9 A major hotel chain keeps a record of the number of mishandled bags per 1,000 customers.In a recent year, the hotel chain had 4.06 mishandled bags per 1,000 customers.Assume that the number of mishandled bags has a Poisson distribution.
-Referring to Scenario 5-9, what is the probability that in the next 1,000 customers, the hotel chain will have no more than three mishandled bags?
(Short Answer)
4.8/5  (30)
(30)
SCENARIO 5-9 A major hotel chain keeps a record of the number of mishandled bags per 1,000 customers.In a recent year, the hotel chain had 4.06 mishandled bags per 1,000 customers.Assume that the number of mishandled bags has a Poisson distribution.
-Referring to Scenario 5-9, what is the probability that in the next 1,000 customers, the hotel chain will have less than two and more than eight mishandled bags?
(Short Answer)
4.7/5  (38)
(38)
SCENARIO 5-9 A major hotel chain keeps a record of the number of mishandled bags per 1,000 customers.In a recent year, the hotel chain had 4.06 mishandled bags per 1,000 customers.Assume that the number of mishandled bags has a Poisson distribution.
-Referring to Scenario 5-9, what is the probability that in the next 1,000 customers, the hotel chain will have at least two mishandled bags?
(Short Answer)
4.8/5  (30)
(30)
The Department of Commerce in a state has determined that the number of small businesses that declare bankruptcy per month is approximately a Poisson distribution with a mean of 6.4.Find the probability that exactly 5 bankruptcies occur next month.
(Short Answer)
4.7/5  (31)
(31)
The expected return of a two-asset portfolio is equal to the product of the weight assigned to the first asset and the expected return of the first asset plus the product of the weight assigned to the second asset and the expected return of the second asset.
(True/False)
4.9/5  (27)
(27)
SCENARIO 5-2 A certain type of new business succeeds 60% of the time.Suppose that 3 such businesses open (where they do not compete, so it is reasonable to believe that their relative successes would be independent).
-Referring to Scenario 5-2, the probability that exactly 1 business succeeds is ________.
(Short Answer)
4.8/5  (29)
(29)
The largest value that a Poisson random variable X can have is n.
(True/False)
4.8/5  (32)
(32)
The expected return of the sum of two investments will be equal to the sum of the expected returns of the two investments plus twice the covariance between the investments.
(True/False)
4.7/5  (38)
(38)
SCENARIO 5-5 From an inventory of 48 new cars being shipped to local dealerships, corporate reports indicate that 12 have defective radios installed.
-Referring to Scenario 5-5, what is the probability out of the 8 new cars it just received that, when each is tested, at least half of the cars have defective radios?
(Short Answer)
4.9/5  (32)
(32)
If X has a binomial distribution with n = 4 and p = 0.3, then 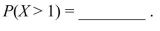
(Short Answer)
4.7/5  (38)
(38)
In a game called Taxation and Evasion, a player rolls a pair of dice.If on any turn the sum is 7, 11, or 12, the player gets audited.Otherwise, she avoids taxes.Suppose a player takes 5 turns at rolling the dice.The standard deviation of the number of times she will be audited is ________.
(Short Answer)
4.8/5  (33)
(33)
SCENARIO 5-1 The probability that a smoke alarm will function properly and sound an alarm in the presence of smoke is 0.8.You have 2 such alarms in your home and they operate independently.
-Referring to Scenario 5-1, the probability that both sound an alarm in the presence of smoke is ________.
(Short Answer)
4.9/5  (40)
(40)
SCENARIO 5-2 A certain type of new business succeeds 60% of the time.Suppose that 3 such businesses open (where they do not compete, so it is reasonable to believe that their relative successes would be independent).
-Referring to Scenario 5-2, the probability that all 3 businesses fail is ________.
(Short Answer)
4.9/5  (28)
(28)
Showing 121 - 140 of 217
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)