Exam 18: A Roadmap for Analyzing Data
Exam 1: Defining and Collecting Data207 Questions
Exam 2: Organizing and Visualizing Variables213 Questions
Exam 3: Numerical Descriptive Measures167 Questions
Exam 4: Basic Probability171 Questions
Exam 5: Discrete Probability Distributions217 Questions
Exam 6: The Normal Distributions and Other Continuous Distributions189 Questions
Exam 7: Sampling Distributions135 Questions
Exam 8: Confidence Interval Estimation189 Questions
Exam 9: Fundamentals of Hypothesis Testing: One-Sample Tests187 Questions
Exam 10: Two-Sample Tests208 Questions
Exam 11: Analysis of Variance216 Questions
Exam 12: Chi-Square and Nonparametric Tests178 Questions
Exam 13: Simple Linear Regression214 Questions
Exam 14: Introduction to Multiple Regression336 Questions
Exam 15: Multiple Regression Model Building99 Questions
Exam 16: Time-Series Forecasting173 Questions
Exam 17: Business Analytics115 Questions
Exam 18: A Roadmap for Analyzing Data329 Questions
Exam 19: Statistical Applications in Quality Management Online162 Questions
Exam 20: Decision Making Online129 Questions
Exam 21: Understanding Statistics: Descriptive and Inferential Techniques39 Questions
Select questions type
SCENARIO 18-10 Given below are results from the regression analysis where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Unemploy)and the independent variables are the age of the worker (Age), the number of years of education received (Edu), the number of years at the previous job (Job Yr), a dummy variable for marital status (Married: 1 = married, 0 = otherwise), a dummy variable for head of household (Head: 1 = yes, 0 = no)and a dummy variable for management position (Manager: 1 = yes, 0 = no).We shall call this Model 1.The coefficient of partial determination  of each of the 6 predictors are, respectively, 0.2807, 0.0386, 0.0317, 0.0141, 0.0958, and 0.1201.
of each of the 6 predictors are, respectively, 0.2807, 0.0386, 0.0317, 0.0141, 0.0958, and 0.1201. 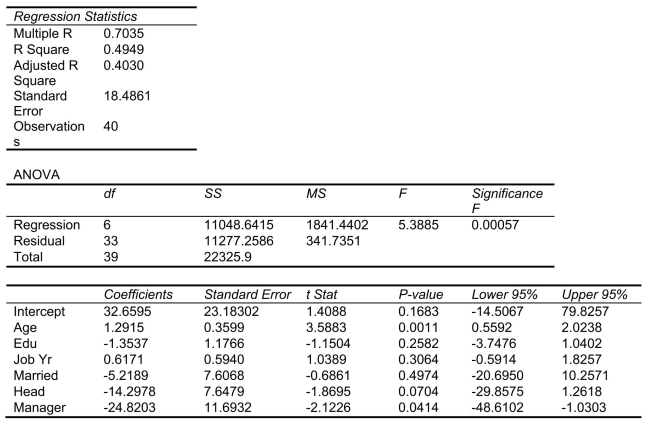 Model 2 is the regression analysis where the dependent variable is Unemploy and the independent variables are Age and Manager.The results of the regression analysis are given below:
Model 2 is the regression analysis where the dependent variable is Unemploy and the independent variables are Age and Manager.The results of the regression analysis are given below: 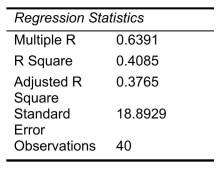
 -Referring to Scenario 18-10 Model 1, which of the following is the correct null hypothesis to test whether age has any effect on the number of weeks a worker is unemployed due to a layoff while holding constant the effect of all the other independent variables?
-Referring to Scenario 18-10 Model 1, which of the following is the correct null hypothesis to test whether age has any effect on the number of weeks a worker is unemployed due to a layoff while holding constant the effect of all the other independent variables?
Free
(Multiple Choice)
4.9/5  (39)
(39)
Correct Answer:
B
SCENARIO 18-1 A real estate builder wishes to determine how house size (House)is influenced by family income (Income), family size (Size), and education of the head of household (School).House size is measured in hundreds of square feet, income is measured in thousands of dollars, and education is in years.The builder randomly selected 50 families and ran the multiple regression.Microsoft Excel output is provided below: SUMMARY OUTPUT  -Referring to Scenario 18-1, the observed value of the F-statistic is missing from the printout.What are the degrees of freedom for this F-statistic?
-Referring to Scenario 18-1, the observed value of the F-statistic is missing from the printout.What are the degrees of freedom for this F-statistic?
Free
(Multiple Choice)
4.9/5  (38)
(38)
Correct Answer:
D
SCENARIO 18-10 Given below are results from the regression analysis where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Unemploy)and the independent variables are the age of the worker (Age), the number of years of education received (Edu), the number of years at the previous job (Job Yr), a dummy variable for marital status (Married: 1 = married, 0 = otherwise), a dummy variable for head of household (Head: 1 = yes, 0 = no)and a dummy variable for management position (Manager: 1 = yes, 0 = no).We shall call this Model 1.The coefficient of partial determination  of each of the 6 predictors are, respectively, 0.2807, 0.0386, 0.0317, 0.0141, 0.0958, and 0.1201.
of each of the 6 predictors are, respectively, 0.2807, 0.0386, 0.0317, 0.0141, 0.0958, and 0.1201.  Model 2 is the regression analysis where the dependent variable is Unemploy and the independent variables are Age and Manager.The results of the regression analysis are given below:
Model 2 is the regression analysis where the dependent variable is Unemploy and the independent variables are Age and Manager.The results of the regression analysis are given below: 
 -Referring to Scenario 18-10 Model 1, what is the standard error of estimate?
-Referring to Scenario 18-10 Model 1, what is the standard error of estimate?
Free
(Short Answer)
4.9/5  (34)
(34)
Correct Answer:
18.4861
Data on the amount of time spent studying and the exam score of 150 students at a high school were collected.You want to know if a student's exam score is linearly related to the amount of time spent on studying.Which of the following would you compute?
(Multiple Choice)
4.8/5  (34)
(34)
The director of admissions at a state college is interested in seeing if admissions status (admitted, waiting list, denied admission)at his college is related to the type of community (urban, rural, suburban)in which an applicant resides.Which of the following tests will be the most appropriate?
(Multiple Choice)
4.7/5  (43)
(43)
The amount of juice that can be squeezed from a randomly selected orange out a box of oranges with approximately the same size can most likely be modeled by which of the following distributions?
(Multiple Choice)
4.9/5  (35)
(35)
SCENARIO 18-9 What are the factors that determine the acceleration time (in sec.)from 0 to 60 miles per hour of a car? Data on the following variables for 171 different vehicle models were collected: Accel Time: Acceleration time in sec. Cargo Vol: Cargo volume in cu.ft. HP: Horsepower MPG: Miles per gallon SUV: 1 if the vehicle model is an SUV with Coupe as the base when SUV and Sedan are both 0 Sedan: 1 if the vehicle model is a sedan with Coupe as the base when SUV and Sedan are both 0 The regression results using acceleration time as the dependent variable and the remaining variables as the independent variables are presented below. SCENARIO 18-9 cont. 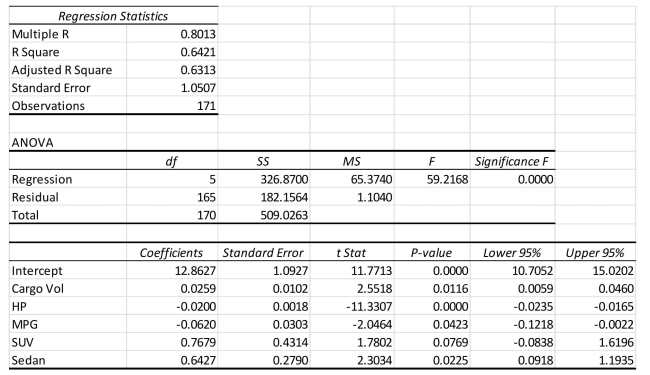 The various residual plots are as shown below.
The various residual plots are as shown below. 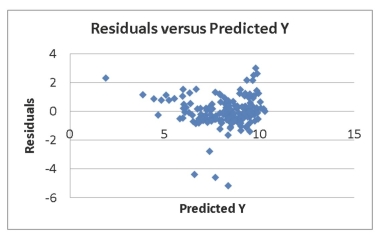 SCENARIO 18-9 cont.
SCENARIO 18-9 cont. 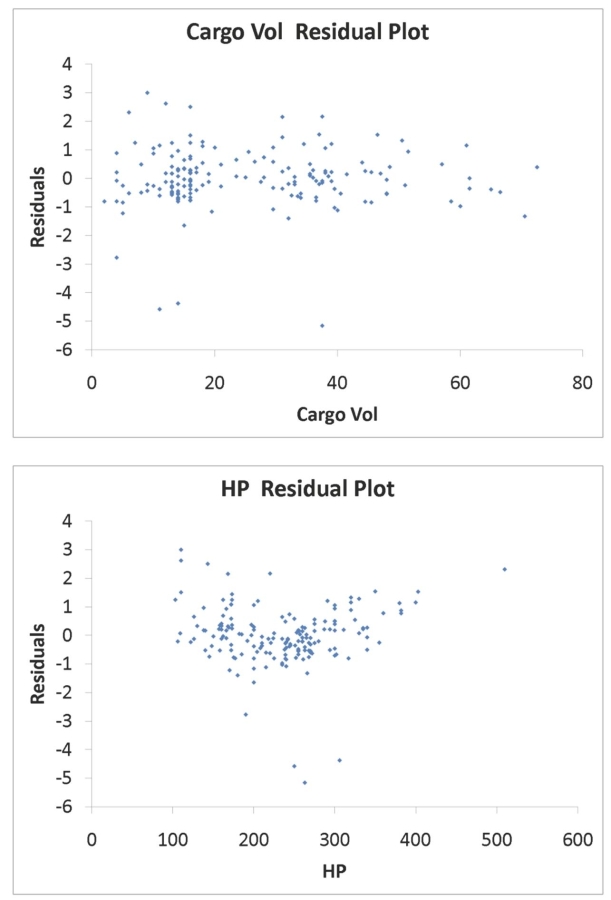 SCENARIO 18-9 cont.
SCENARIO 18-9 cont. 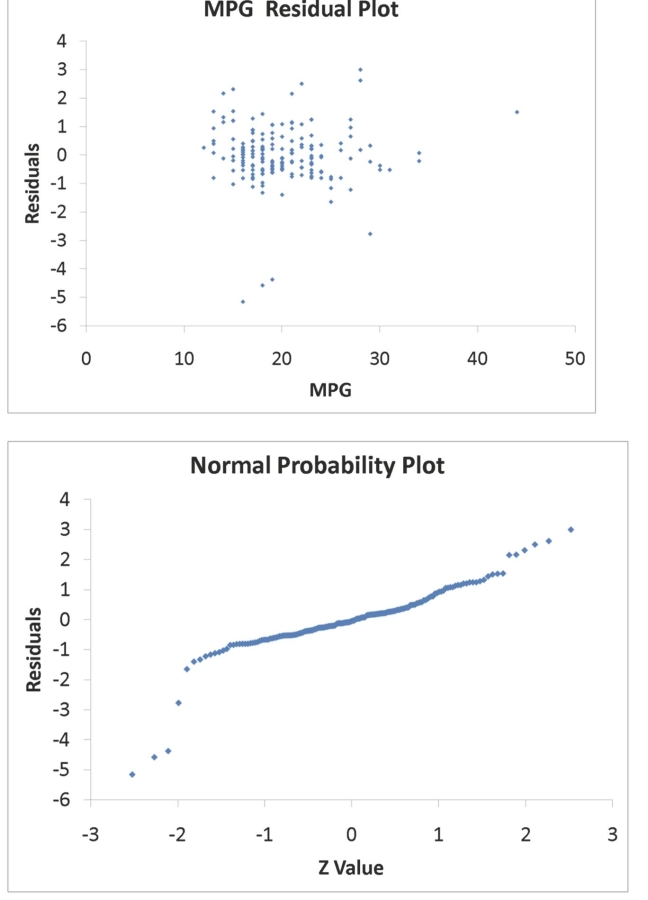 The coefficient of partial determination
The coefficient of partial determination  of each of the 5 predictors are, respectively, 0.0380, 0.4376, 0.0248, 0.0188, and 0.0312. The coefficient of multiple determination for the regression model using each of the 5 variables
of each of the 5 predictors are, respectively, 0.0380, 0.4376, 0.0248, 0.0188, and 0.0312. The coefficient of multiple determination for the regression model using each of the 5 variables 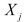 as the dependent variable and all other X variables as independent variables (
as the dependent variable and all other X variables as independent variables ( 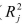 )are, respectively, 0.7461, 0.5676, 0.6764, 0.8582, 0.6632.
-Referring to Scenario 18-9, what is the correct interpretation for the estimated coefficient for Sedan?
)are, respectively, 0.7461, 0.5676, 0.6764, 0.8582, 0.6632.
-Referring to Scenario 18-9, what is the correct interpretation for the estimated coefficient for Sedan?
(Multiple Choice)
4.7/5  (34)
(34)
SCENARIO 18-12 The marketing manager for a nationally franchised lawn service company would like to study the characteristics that differentiate home owners who do and do not have a lawn service.A random sample of 30 home owners located in a suburban area near a large city was selected; 15 did not have a lawn service (code 0)and 15 had a lawn service (code 1).Additional information available concerning these 30 home owners includes family income (Income, in thousands of dollars), lawn size (Lawn Size, in thousands of square feet), attitude toward outdoor recreational activities (Attitude 0 = unfavorable, 1 = favorable), number of teenagers in the household (Teenager), and age of the head of the household (Age). The Minitab output is given below: 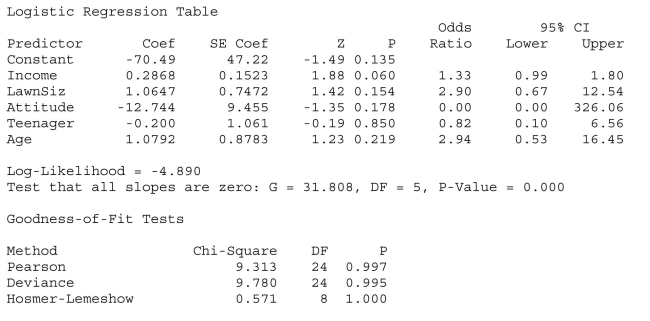 -Referring to Scenario 18-12, what are the degrees of freedom for the chi-square distribution when testing whether the model is a good-fitting model?
-Referring to Scenario 18-12, what are the degrees of freedom for the chi-square distribution when testing whether the model is a good-fitting model?
(Short Answer)
4.9/5  (36)
(36)
SCENARIO 18-10 Given below are results from the regression analysis where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Unemploy)and the independent variables are the age of the worker (Age), the number of years of education received (Edu), the number of years at the previous job (Job Yr), a dummy variable for marital status (Married: 1 = married, 0 = otherwise), a dummy variable for head of household (Head: 1 = yes, 0 = no)and a dummy variable for management position (Manager: 1 = yes, 0 = no).We shall call this Model 1.The coefficient of partial determination  of each of the 6 predictors are, respectively, 0.2807, 0.0386, 0.0317, 0.0141, 0.0958, and 0.1201.
of each of the 6 predictors are, respectively, 0.2807, 0.0386, 0.0317, 0.0141, 0.0958, and 0.1201.  Model 2 is the regression analysis where the dependent variable is Unemploy and the independent variables are Age and Manager.The results of the regression analysis are given below:
Model 2 is the regression analysis where the dependent variable is Unemploy and the independent variables are Age and Manager.The results of the regression analysis are given below: 
 -Referring to Scenario 18-10 Model 1, which of the following is a correct statement?
-Referring to Scenario 18-10 Model 1, which of the following is a correct statement?
(Multiple Choice)
4.9/5  (28)
(28)
An agronomist wants to compare the crop yield of 3 varieties of chickpea seeds.She plants all 3 varieties of the seeds on each of 5 different patches of fields.She then measures the crop yield in bushels per acre.Which of the following tests will be the most appropriate to find out if there is any difference in crop yield among the 3 varieties?
(Multiple Choice)
4.8/5  (41)
(41)
SCENARIO 18-6 A weight-loss clinic wants to use regression analysis to build a model for weight-loss of a client (measured in pounds).Two variables thought to affect weight-loss are client's length of time on the weight loss program and time of session.These variables are described below: Y = Weight-loss (in pounds) 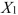 = Length of time in weight-loss program (in months)
= Length of time in weight-loss program (in months) 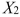 = 1 if morning session, 0 if not
= 1 if morning session, 0 if not 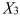 = 1 if afternoon session, 0 if not (Base level = evening session) Data for 12 clients on a weight-loss program at the clinic were collected and used to fit the interaction model:
= 1 if afternoon session, 0 if not (Base level = evening session) Data for 12 clients on a weight-loss program at the clinic were collected and used to fit the interaction model: 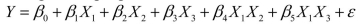 Partial output from Microsoft Excel follows:
Partial output from Microsoft Excel follows: 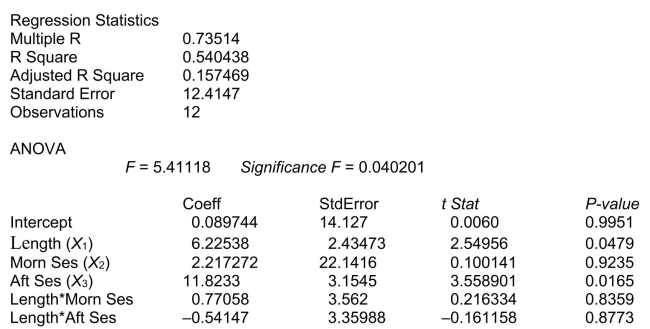 -Referring to Scenario 18-6, in terms of the
-Referring to Scenario 18-6, in terms of the 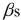 in the model, give the mean change in weight-loss (Y)for every 1 month increase in time in the program (
in the model, give the mean change in weight-loss (Y)for every 1 month increase in time in the program ( 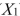 when attending the morning session.
when attending the morning session.
(Multiple Choice)
4.9/5  (33)
(33)
A debate team of 4 members for a high school will be chosen randomly from a potential group of 15 students.Ten of the 15 students have no prior competition experience while the others have some degree of experience.Which of the following distributions would you use to determine the probability that none of the members chosen for the team have any competition experience?
(Multiple Choice)
4.7/5  (37)
(37)
SCENARIO 18-10 Given below are results from the regression analysis where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Unemploy)and the independent variables are the age of the worker (Age), the number of years of education received (Edu), the number of years at the previous job (Job Yr), a dummy variable for marital status (Married: 1 = married, 0 = otherwise), a dummy variable for head of household (Head: 1 = yes, 0 = no)and a dummy variable for management position (Manager: 1 = yes, 0 = no).We shall call this Model 1.The coefficient of partial determination  of each of the 6 predictors are, respectively, 0.2807, 0.0386, 0.0317, 0.0141, 0.0958, and 0.1201.
of each of the 6 predictors are, respectively, 0.2807, 0.0386, 0.0317, 0.0141, 0.0958, and 0.1201.  Model 2 is the regression analysis where the dependent variable is Unemploy and the independent variables are Age and Manager.The results of the regression analysis are given below:
Model 2 is the regression analysis where the dependent variable is Unemploy and the independent variables are Age and Manager.The results of the regression analysis are given below: 
 -Referring to Scenario 18-10 and using both Model 1 and Model 2, what are the degrees of freedom of the test statistic for testing whether the independent variables that are not significant individually are also not significant as a group in explaining the variation in the dependent variable at a 5% level of significance?
-Referring to Scenario 18-10 and using both Model 1 and Model 2, what are the degrees of freedom of the test statistic for testing whether the independent variables that are not significant individually are also not significant as a group in explaining the variation in the dependent variable at a 5% level of significance?
(Short Answer)
4.7/5  (42)
(42)
SCENARIO 18-12 The marketing manager for a nationally franchised lawn service company would like to study the characteristics that differentiate home owners who do and do not have a lawn service.A random sample of 30 home owners located in a suburban area near a large city was selected; 15 did not have a lawn service (code 0)and 15 had a lawn service (code 1).Additional information available concerning these 30 home owners includes family income (Income, in thousands of dollars), lawn size (Lawn Size, in thousands of square feet), attitude toward outdoor recreational activities (Attitude 0 = unfavorable, 1 = favorable), number of teenagers in the household (Teenager), and age of the head of the household (Age). The Minitab output is given below:  -Referring to Scenario 18-12, what should be the decision ('reject' or 'do not reject')on the null hypothesis when testing whether Teenager makes a significant contribution to the model in the presence of the other independent variables at a 0.05 level of significance?
-Referring to Scenario 18-12, what should be the decision ('reject' or 'do not reject')on the null hypothesis when testing whether Teenager makes a significant contribution to the model in the presence of the other independent variables at a 0.05 level of significance?
(Short Answer)
4.8/5  (31)
(31)
SCENARIO 18-8 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing), daily mean of the percentage of students attending class (% Attendance), mean teacher salary in dollars (Salaries), and instructional spending per pupil in dollars (Spending)of 47 schools in the state. Following is the multiple regression output with 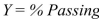 as the dependent variable,
as the dependent variable, 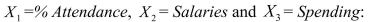
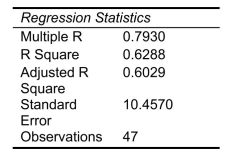
 -Referring to Scenario 18-8, you can conclude that instructional spending per pupil individually has no impact on the mean percentage of students passing the proficiency test, considering the effect of all the other independent variables, at a 10% level of significance based solely on the 95% confidence interval estimate for
-Referring to Scenario 18-8, you can conclude that instructional spending per pupil individually has no impact on the mean percentage of students passing the proficiency test, considering the effect of all the other independent variables, at a 10% level of significance based solely on the 95% confidence interval estimate for 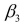 .
.
(True/False)
4.9/5  (37)
(37)
SCENARIO 18-10 Given below are results from the regression analysis where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Unemploy)and the independent variables are the age of the worker (Age), the number of years of education received (Edu), the number of years at the previous job (Job Yr), a dummy variable for marital status (Married: 1 = married, 0 = otherwise), a dummy variable for head of household (Head: 1 = yes, 0 = no)and a dummy variable for management position (Manager: 1 = yes, 0 = no).We shall call this Model 1.The coefficient of partial determination  of each of the 6 predictors are, respectively, 0.2807, 0.0386, 0.0317, 0.0141, 0.0958, and 0.1201.
of each of the 6 predictors are, respectively, 0.2807, 0.0386, 0.0317, 0.0141, 0.0958, and 0.1201.  Model 2 is the regression analysis where the dependent variable is Unemploy and the independent variables are Age and Manager.The results of the regression analysis are given below:
Model 2 is the regression analysis where the dependent variable is Unemploy and the independent variables are Age and Manager.The results of the regression analysis are given below: 
 -Referring to Scenario 18-10 Model 1, we can conclude that, holding constant the effect of the other independent variables, the number of years of education received has no impact on the mean number of weeks a worker is unemployed due to a layoff at a 10% level of significance if all we have is the information on the 95% confidence interval estimate for
-Referring to Scenario 18-10 Model 1, we can conclude that, holding constant the effect of the other independent variables, the number of years of education received has no impact on the mean number of weeks a worker is unemployed due to a layoff at a 10% level of significance if all we have is the information on the 95% confidence interval estimate for 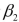 .
.
(True/False)
4.9/5  (32)
(32)
SCENARIO 18-10 Given below are results from the regression analysis where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Unemploy)and the independent variables are the age of the worker (Age), the number of years of education received (Edu), the number of years at the previous job (Job Yr), a dummy variable for marital status (Married: 1 = married, 0 = otherwise), a dummy variable for head of household (Head: 1 = yes, 0 = no)and a dummy variable for management position (Manager: 1 = yes, 0 = no).We shall call this Model 1.The coefficient of partial determination  of each of the 6 predictors are, respectively, 0.2807, 0.0386, 0.0317, 0.0141, 0.0958, and 0.1201.
of each of the 6 predictors are, respectively, 0.2807, 0.0386, 0.0317, 0.0141, 0.0958, and 0.1201.  Model 2 is the regression analysis where the dependent variable is Unemploy and the independent variables are Age and Manager.The results of the regression analysis are given below:
Model 2 is the regression analysis where the dependent variable is Unemploy and the independent variables are Age and Manager.The results of the regression analysis are given below: 
 -Referring to Scenario 18-10 and using both Model 1 and Model 2, there is sufficient evidence to conclude that the independent variables that are not significant individually are also not significant as a group in explaining the variation in the dependent variable at a 5% level of significance?
-Referring to Scenario 18-10 and using both Model 1 and Model 2, there is sufficient evidence to conclude that the independent variables that are not significant individually are also not significant as a group in explaining the variation in the dependent variable at a 5% level of significance?
(True/False)
4.9/5  (38)
(38)
SCENARIO 18-8 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing), daily mean of the percentage of students attending class (% Attendance), mean teacher salary in dollars (Salaries), and instructional spending per pupil in dollars (Spending)of 47 schools in the state. Following is the multiple regression output with 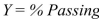 as the dependent variable,
as the dependent variable, 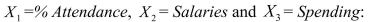

 -Referring to Scenario 18-8, the null hypothesis
-Referring to Scenario 18-8, the null hypothesis 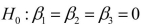 implies that percentage of students passing the proficiency test is not affected by some of the explanatory variables.
implies that percentage of students passing the proficiency test is not affected by some of the explanatory variables.
(True/False)
4.7/5  (40)
(40)
SCENARIO 18-3 A financial analyst wanted to examine the relationship between salary (in $1,000)and 4 variables: age ( 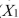 = Age), experience in the field (
= Age), experience in the field ( 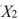 = Exper), number of degrees (
= Exper), number of degrees ( 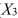 = Degrees), and number of previous jobs in the field (
= Degrees), and number of previous jobs in the field ( 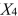 = Prevjobs).He took a sample of 20 employees and obtained the following Microsoft Excel output: SUMMARY OUTPUT
= Prevjobs).He took a sample of 20 employees and obtained the following Microsoft Excel output: SUMMARY OUTPUT 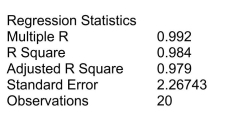
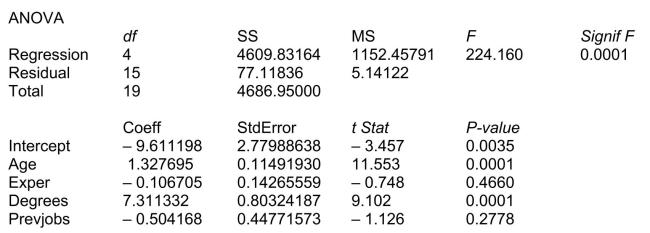 -Referring to Scenario 18-3, the net regression coefficient of
-Referring to Scenario 18-3, the net regression coefficient of 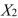 is ________.
is ________.
(Short Answer)
4.9/5  (37)
(37)
SCENARIO 18-8 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing), daily mean of the percentage of students attending class (% Attendance), mean teacher salary in dollars (Salaries), and instructional spending per pupil in dollars (Spending)of 47 schools in the state. Following is the multiple regression output with 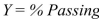 as the dependent variable,
as the dependent variable, 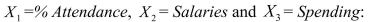

 -Referring to Scenario 18-8, there is sufficient evidence that all of the explanatory variables are related to the percentage of students passing the proficiency test at a 5% level of significance.
-Referring to Scenario 18-8, there is sufficient evidence that all of the explanatory variables are related to the percentage of students passing the proficiency test at a 5% level of significance.
(True/False)
4.8/5  (33)
(33)
Showing 1 - 20 of 329
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)