Exam 11: Inference About a Population

The air pumps at service stations come equipped with a gauge to regulate the air pressure of tires. A mechanic believes that the gauges are in error by at least 3 pounds per square inch. To test his belief he takes a random example of 50 air pump gauges and determines the difference between the true pressure (as measured by an accurate measuring device)and the pressure shown on the air pump gauge. The mean and the standard deviation of the sample are 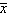= 3.4 and s = 1.2. Can the mechanic infer that he is correct at the 5% significance level? Assume tire pressures have a normal distribution.

A random sample of 25 observations is selected from a normally distributed population. The sample variance is 10. In the 95% confidence interval for the population variance, the upper limit is:

The chi-squared distribution can be used in constructing confidence intervals and carrying out hypothesis tests regarding the value of a population variance.

Energy Drink Consumption A researcher at the University of Washington medical school believes that energy drink consumption may increase heart rate. Suppose it is known that heart rate (in beats per minute)is normally distributed with an average of 70 bpm for adults. A random sample of 25 adults was selected and it was found that their average heartbeat was 73 bpm after energy drink consumption, with a standard deviation of 7 bpm. {Energy Drink Consumption Narrative} Test the hypotheses in the previous question at the 10% significance level to determine if we can infer that energy drink consumption increases heart rate.

A major electronics store chain is interested in estimating the average amount its credit card customers spent on their first visit to the chain's new store in the mall. Fifteen credit card accounts were randomly sampled and analyzed with the following results: 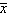= $50.50 and s ² = 400. A 95% confidence interval for the average amount the credit card customers spent on their first visit to the chain's new store in the mall is:

The area to the right of a certain critical value on a chi-squared distribution is 0.025. For 5 degrees of freedom, the critical value is 11.143.

The test statistic used to test hypotheses about the population variance is given by c ² = ( n - 1)s ² \ s ², which is chi-squared distributed with n - 1 degrees of freedom when the population is normally distributed with variance equal to s ² .

Which of the following conditions is needed regarding the chi-squared test statistic for the test of variance?

Researchers determined that 60 Puffs tissues is the average number of tissues used during a cold. Suppose a random sample of 100 Puffs users yielded the following data on the number of tissues used during a cold: 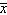= 52 and s = 22. Suppose the alternative we wanted to test was H ₁: m a = 0.05 is:

A random sample of size 15 taken from a normally distributed population revealed a sample mean of 75 and a sample variance of 25. The upper limit of a 95% confidence interval for the population mean would equal:

Researchers determined that 60 Puffs tissues is the average number of tissues used during a cold. Suppose a random sample of 100 Puffs users yielded the following data on the number of tissues used during a cold: 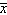= 52 and s = 22. Suppose the test statistic does not fall in the rejection region at a = 0.05. Which of the following conclusions is correct?

The t -test for a population mean is ____________________, meaning that if the population is nonnormal, the results of the test and confidence interval are still valid as long as the nonnormality is not extreme.

Applicants' Grades The grades of a sample of 10 applicants, selected at random from a large population, are 71, 86, 75, 63, 92, 70, 81, 59, 80, and 90. {Applicants' Grades Narrative} Construct a 90% confidence interval estimate for the population standard deviation.

The t- distribution allows the calculation of confidence intervals for means for small samples when the population variance is not known, regardless of the shape of the distribution in the population.

Two uses for the population variance are to measure risk and consistency.

The statistic ( n - 1)s ² \ s ² has a chi-squared distribution with n - 1 degrees of freedom if:

A pharmaceutical company has just developed a new capsule to alleviate the symptoms of allergies and colds. However, they are concerned about the variability in the amount of time until the drug becomes effective. In a random sample of 10 individuals who suffer from allergies, the amount of time (in hours)for the capsule to take effect was recorded and listed as follows: 5, 7, 6, 10, 9, 12, 8, 17, 4, and 16. Estimate with 90% confidence the variance of the time for the drug to become effective.

Because of the greater uncertainty, the t -statistic will display greater ____________________ than the z -statistic.

A race car driver tested his car for time from 0 to 60 mph, and in 20 tests obtained an average of 48.5 seconds with a standard deviation of 1.47 seconds. A 95% confidence interval for the 0 to 60 time is 45.2 seconds to 51.8 seconds.

Single Mothers' Ages A random sample of 10 single mothers was drawn from a Obstetrics Clinic. Their ages are 22, 17, 27, 20, 23, 19, 24, 18, 19, and 24 years. {Single Mothers' Ages Narrative} What is the required condition of the techniques used in the previous questions? What graphical device can you use to check to see if that required condition is satisfied?