Question 1

The probability of an event is the ____________________ of the probabilities of the simple events that constitute the event.

Accepted Answer

sum

Question 2

If A and B are any two events with P ( A )= .8 and P ( B|A c)= .7, then P ( Ac and B )is

Accepted Answer

A) 0.56 
B) 0.14 
C) 1.50 
D) None of these choices. 
A) 0.56 
B) 0.14 
C) 1.50 
D) None of these choices. B

Question 3

The conditional probability of event B given event A is denoted by P ( A | B ).

Accepted Answer

A) True 
 B)False  False

Question 4

The outcomes of a sample space must be ____________________, which means that all possible outcomes must be included.

Accepted Answer

The answer of The outcomes of a sample space must...

Question 5

Two events A and B are said to be independent if P ( A|B )= P ( B ).

Accepted Answer

A) True 
 B)False

Question 6

Drunk Drivers Five hundred accidents that occurred on a Saturday night were analyzed. Two items noted were the number of vehicles involved and whether alcohol played a role in the accident. The numbers are shown below: 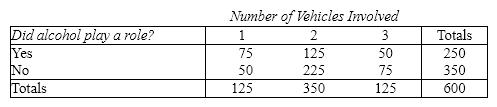  {Drunk Drivers Narrative} If multiple vehicles were involved, what proportion of accidents involved alcohol?

Accepted Answer

The answer of Drunk Drivers Five hundred accidents that occurred...

Question 7

A random experiment is an action or process that leads to one of several possible ____________________.

Accepted Answer

The answer of A random experiment is an action or...

Question 8

Cysts After researching cysts of a particular type, a doctor learns that out of 10,000 such cysts examined, 1,500 are malignant and 8,500 are benign. A diagnostic test is available which is accurate 80% of the time (whether the cyst is malignant or not). The doctor has discovered the same type of cyst in a patient. {Cysts Narrative} What is the probability that the patient will test negative?

Accepted Answer

P ( - )= 1 - P (+)= 1 - .29 =

Question 9

If A and B are independent, then P ( A | B )= P ( A )or P ( B | A )= P ( B ).

Accepted Answer

A) True 
 B)False

Question 10

If P ( A )= 0.25 and P ( B )= 0.65, then P ( A and B )is:

Accepted Answer

A) 0.25 
B) 0.40 
C) 0.90 
D) cannot be determined from the information given 
A) 0.25 
B) 0.40 
C) 0.90 
D) cannot be determined from the information given

Question 11

A(n)____________________ of a random experiment is a list of all possible outcomes of the experiment.

Accepted Answer

The answer of A(n)____________________ of a random experiment is a...

Question 12

The probability of the intersection is called a joint probability.

Accepted Answer

A) True 
 B)False

Question 13

Messenger Service Three messenger services deliver to a small town in Oregon. Service A has 60% of all the scheduled deliveries, service B has 30%, and service C has the remaining 10%. Their on-time rates are 80%, 60%, and 40% respectively. Define event O as a service delivers a package on time. {Messenger Service Narrative} If a package was delivered on time, what is the probability that it was service A ?

Accepted Answer

P ( A | O )= P ( A a

Question 14

If A and B are independent events with P ( A )= 0.20 and P ( B )= 0.60, then P ( A | B )is:

Accepted Answer

A) 0.20 
B) 0.60 
C) 0.40 
D) 0.80 
A) 0.20 
B) 0.60 
C) 0.40 
D) 0.80

Question 15

Financial Consultants A Financial Consultant has classified his clients according to their gender and the composition of their investment portfolio (primarily bonds, primarily stocks, or a balanced mix of bonds and stocks). The proportions of clients falling into the various categories are shown in the following table: 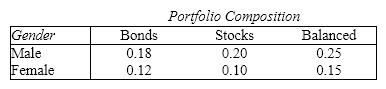  One client is selected at random, and two events A and B are defined as follows: A : The client selected is male. B : The client selected has a balanced portfolio. {Financial Consultants Narrative} Find the following probabilities: 
 a. P ( A|B )
 b. P ( B|A )

Accepted Answer

a. 0.625

Question 16

If A and B are any two events with P ( A )= .8 and P ( B|A )= .4, then P ( A and B )is:

Accepted Answer

A) .40 
B) .32 
C) 1.20 
D) None of these choices. 
A) .40 
B) .32 
C) 1.20 
D) None of these choices.

Question 17

Certification Test A standard certification test was given at three locations. 1,000 candidates took the test at location A , 600 candidates at location B , and 400 candidates at location C . The percentages of candidates from locations A , B , and C who passed the test were 70%, 68%, and 77%, respectively. One candidate is selected at random from among those who took the test. {Certification Test Narrative} What is the probability that the selected candidate passed the test?

Accepted Answer

(.5)(.7)+

Question 18

{Certification Test Narrative} What is the probability that the selected candidate took the test at location C and failed?

Accepted Answer

The answer of {Certification Test Narrative} What is the probability...

Question 19

Construction Bids A construction company has submitted bids on two separate state contracts, A and B . The company feels that it has a 60% chance of winning contract A , and a 50% chance of winning contract B . Furthermore, the company believes that it has an 80% chance of winning contract A if it wins contract B . {Construction Bids Narrative} What is the probability that the company will win at least one of the two contracts?

Accepted Answer

P ( A or B )= P ( A

Question 20

Two or more events are said to be independent when the occurrence of one event has no effect on the probability that another will occur.

Accepted Answer

A) True 
 B)False

The probability of an event is the ____________________ of the probabilities of the simple events that constitute the event.

If A and B are any two events with P ( A )= .8 and P ( B|A ^c)= .7, then P ( A^c and B )is

The conditional probability of event B given event A is denoted by P ( A | B ).

The outcomes of a sample space must be ____________________, which means that all possible outcomes must be included.

Two events A and B are said to be independent if P ( A|B )= P ( B ).

A random experiment is an action or process that leads to one of several possible ____________________.

If A and B are independent, then P ( A | B )= P ( A )or P ( B | A )= P ( B ).

If P ( A )= 0.25 and P ( B )= 0.65, then P ( A and B )is:

A(n)____________________ of a random experiment is a list of all possible outcomes of the experiment.

The probability of the intersection is called a joint probability.

If A and B are independent events with P ( A )= 0.20 and P ( B )= 0.60, then P ( A | B )is:

If A and B are any two events with P ( A )= .8 and P ( B|A )= .4, then P ( A and B )is:

{Certification Test Narrative} What is the probability that the selected candidate took the test at location C and failed?

Two or more events are said to be independent when the occurrence of one event has no effect on the probability that another will occur.

What Is Statistics

Graphical and Tabular Descriptive Techniques

Numerical Descriptive Techniques

Data Collection and Sampling

Random Variables and Discrete Probability Distributions

Continuous Probability Distributions

Sampling Distributions

Introduction to Estimation

Introduction to Hypothesis Testing

Inference About a Population

Inference About Comparing Two Populat

Inference About Comparing Two Populat

Analysis of Variance

Chi-Squared Tests

Simple Linear Regression and Correlat

Multiple Regression

Review of Statistical Inference

Filters

Exam 5: Probability

The probability of an event is the ____________________ of the probabilities of the simple events that constitute the event.

If A and B are any two events with P ( A )= .8 and P ( B|A c)= .7, then P ( Ac and B )is

The conditional probability of event B given event A is denoted by P ( A | B ).

The outcomes of a sample space must be ____________________, which means that all possible outcomes must be included.

Two events A and B are said to be independent if P ( A|B )= P ( B ).

A random experiment is an action or process that leads to one of several possible ____________________.

If A and B are independent, then P ( A | B )= P ( A )or P ( B | A )= P ( B ).

If P ( A )= 0.25 and P ( B )= 0.65, then P ( A and B )is:

A(n)____________________ of a random experiment is a list of all possible outcomes of the experiment.

The probability of the intersection is called a joint probability.

If A and B are independent events with P ( A )= 0.20 and P ( B )= 0.60, then P ( A | B )is:

If A and B are any two events with P ( A )= .8 and P ( B|A )= .4, then P ( A and B )is:

{Certification Test Narrative} What is the probability that the selected candidate took the test at location C and failed?

Two or more events are said to be independent when the occurrence of one event has no effect on the probability that another will occur.

What Is Statistics

Graphical and Tabular Descriptive Techniques

Numerical Descriptive Techniques

Data Collection and Sampling

Random Variables and Discrete Probability Distributions

Continuous Probability Distributions

Sampling Distributions

Introduction to Estimation

Introduction to Hypothesis Testing

Inference About a Population

Inference About Comparing Two Populat

Inference About Comparing Two Populat

Analysis of Variance

Chi-Squared Tests

Simple Linear Regression and Correlat

Multiple Regression

Review of Statistical Inference

Filters

If A and B are any two events with P ( A )= .8 and P ( B|A ^c)= .7, then P ( A^c and B )is