Question 1

All of the expected frequencies in a chi-squared goodness-of-fit test must be equal to each other.

Accepted Answer

A) True 
 B)False  False

Question 2

Student Absenteeism Consider a multinomial experiment involving n = 200 students of a large high school. The attendance department recorded the number of students who were absent during the weekdays. The null hypothesis to be tested is: H 0: p 1 = 0.10, p 2 = 0.25, p 3 = 0.30, p 4 = 0.20, p 5 = 0.15. {Student Absenteeism Narrative} Test the hypothesis at the 5% level of significance with the following frequencies:

Accepted Answer

Rejection region: c ² > c ²_0.05,4 = 9.488 Test statistic: c ² = 1.147 Conclusion: Cannot reject the null hypothesis. There is not enough evidence to conclude that absenteeism patterns differ throughout the week.

Question 3

To determine whether a single coin is fair, the coin was tossed 200 times. The observed frequencies with which each of the two sides of the coin turned up are recorded as 112 heads and 88 tails. Is the coin fair?

Accepted Answer

H ₀: p ₁ = 0.50, p ₂ = 0.50 (the coin is fair)H ₁: At least one p_i is not equal to its specified value (the coin is not fair)Rejection region: c ² > c ²_0.05,1 = 3.841 Test statistic: c ² = 2.88 Conclusion: Cannot reject the null hypothesis. There is not enough evidence to say the coin is not fair, according to the data.

Question 4

In the test of a contingency table, the expected cell frequencies must satisfy the rule of 5.

Accepted Answer

A) True 
 B)False

Question 5

In 2011, the student body of a state university in Alabama consists of 30% freshmen, 25% sophomores, 27% juniors, and 18% seniors. A sample of 400 students taken from the 2012 student body showed that there are 138 freshmen, 88 sophomores, 94 juniors, and 80 seniors. Test with 5% significance level to determine whether the student body proportions have changed.

Accepted Answer

H ₀: p ₁ = 0.30, p ₂ =0.25, p ₃ = 0.27, p ₄ =

Question 6

If there are only two categories, the chi-squared goodness-of-fit test is the same as the z -test for p , the population proportion (as long as the sample\cell sizes meet the conditions).

Accepted Answer

A) True 
 B)False

Question 7

A calculus professor posted the following grade distribution guidelines for her elementary calculus class: 8% A, 35% B, 40% C, 12% D, and 5% F. A sample of 100 elementary statistics grades at the end of last semester showed 12 As, 30 Bs, 35 Cs, 15 Ds, and 8 Fs. Test at the 5% significance level to determine whether the actual grades deviate significantly from the posted grade distribution guidelines.

Accepted Answer

H ₀: p ₁ = 0.08, p ₂ = 0.35, p ₃ = 0.40, p ₄

Question 8

A chi-squared test statistic in a test of a contingency table that is equal to zero means:

Accepted Answer

A) The two nominal variables are equal. 
B) The two nominal variables are independent. 
C) The two nominal variables have the same proportions listed in H 0. 
D) All of these choices. 
A) The two nominal variables are equal. 
B) The two nominal variables are independent. 
C) The two nominal variables have the same proportions listed in H 0. 
D) All of these choices.

Question 9

Seat Belts A study was conducted to determine whether the use of seat belts in vehicles depends on whether or not a child was present in the car. A sample of 1,000 people treated for injuries sustained from vehicle accidents was obtained, and each person was classified according to (1)child present (yes
o)and (2)seat belt usage (worn or not worn)during the accident. The data are shown in the table below. 
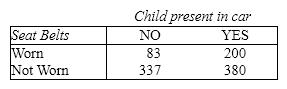   {Seat Belts Narrative} Calculate the value of the test statistic.

Accepted Answer

The answer of Seat Belts A study was conducted to...

Question 10

Which of the following conditions indicate that H 0 should be rejected in a goodness-of-fit test?

Accepted Answer

A) The observed frequencies are equal to their expected frequencies. 
B) The test statistic is large. 
C) The degrees of freedom is large. 
D) All of these choices are true. 
A) The observed frequencies are equal to their expected frequencies. 
B) The test statistic is large. 
C) The degrees of freedom is large. 
D) All of these choices are true.

Question 11

Consider a multinomial experiment involving 100 trials and 3 categories (cells). The observed frequencies resulting from the experiment are shown in the accompanying table. 
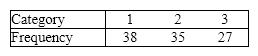   Use the 5% significance level to test the hypotheses H 0: p 1 = 0.45, p 2 = 0.30, p 3 = 0.25 vs. H 1: At least two proportions differ from their specified values.

Accepted Answer

Rejection region: c ² > c ²_0.10,3 = 5.991 Test s

Question 12

A chi-squared goodness-of-fit test is always conducted as a(n):

Accepted Answer

A) lower-tail test. 
B) upper-tail test. 
C) two-tail test. 
D) All of these choices are true. 
A) lower-tail test. 
B) upper-tail test. 
C) two-tail test. 
D) All of these choices are true.

Question 13

A chi-squared test of a contingency table is applied to a contingency table with 4 rows and 4 columns for two qualitative variables. The degrees of freedom for this test must be 9.

Accepted Answer

A) True 
 B)False

Question 14

A sports preference poll showed the following data for adults and children: 
     Use the 5% level of significance and test to determine whether sports preferences depend on age group.

Accepted Answer

H ₀: Age group and sports preferences are

Question 15

To determine the critical values in the chi-squared distribution table, you need to know the:

Accepted Answer

A) sample size. 
B) degrees of freedom 
C) probability of Type II error. 
D) All of these choices are true. 
A) sample size. 
B) degrees of freedom 
C) probability of Type II error. 
D) All of these choices are true.

Question 16

The expected values of a contingency table are calculated based on the assumption that H 0 is ____________________.

Accepted Answer

Question 17

Explain what is meant by the rule of five and what you should do if this rule is not met.

Accepted Answer

The rule of five requires that the expec

Question 18

How do you find the probabilities needed to obtain expected frequencies for a test of a contingency table?

Accepted Answer

A) If there are r rows and c columns, let each probability be 1\ rc . 
B) Use the probabilities specified in the null hypothesis. 
C) Assume H 0 is true and use your data to calculate them. 
D) None of these choices. 
A) If there are r rows and c columns, let each probability be 1\ rc . 
B) Use the probabilities specified in the null hypothesis. 
C) Assume H 0 is true and use your data to calculate them. 
D) None of these choices.

Question 19

In the test of a contingency table, the observed cell frequencies must satisfy the rule of 5.

Accepted Answer

A) True 
 B)False

Question 20

Suppose the value of your chi-squared test statistic in a goodness-of-fit test is equal to 0. What do you conclude?

Accepted Answer

A) Reject H 0. Conclude that at least one proportion is not equal to its specified value. 
B) Fail to reject H 0. Not enough evidence to say the proportions are different from what is listed in H 0. 
C) Not enough information; need the degrees of freedom for the test. 
D) None of these choices. 
A) Reject H 0. Conclude that at least one proportion is not equal to its specified value. 
B) Fail to reject H 0. Not enough evidence to say the proportions are different from what is listed in H 0. 
C) Not enough information; need the degrees of freedom for the test. 
D) None of these choices.

All of the expected frequencies in a chi-squared goodness-of-fit test must be equal to each other.

To determine whether a single coin is fair, the coin was tossed 200 times. The observed frequencies with which each of the two sides of the coin turned up are recorded as 112 heads and 88 tails. Is the coin fair?

In the test of a contingency table, the expected cell frequencies must satisfy the rule of 5.

If there are only two categories, the chi-squared goodness-of-fit test is the same as the z -test for p , the population proportion (as long as the sample\cell sizes meet the conditions).

A chi-squared test statistic in a test of a contingency table that is equal to zero means:

Which of the following conditions indicate that H ₀ should be rejected in a goodness-of-fit test?

A chi-squared goodness-of-fit test is always conducted as a(n):

A chi-squared test of a contingency table is applied to a contingency table with 4 rows and 4 columns for two qualitative variables. The degrees of freedom for this test must be 9.

A sports preference poll showed the following data for adults and children: Use the 5% level of significance and test to determine whether sports preferences depend on age group.

To determine the critical values in the chi-squared distribution table, you need to know the:

The expected values of a contingency table are calculated based on the assumption that H ₀ is ____________________.

Explain what is meant by the rule of five and what you should do if this rule is not met.

How do you find the probabilities needed to obtain expected frequencies for a test of a contingency table?

In the test of a contingency table, the observed cell frequencies must satisfy the rule of 5.

Suppose the value of your chi-squared test statistic in a goodness-of-fit test is equal to 0. What do you conclude?

What Is Statistics

Graphical and Tabular Descriptive Techniques

Numerical Descriptive Techniques

Data Collection and Sampling

Probability

Random Variables and Discrete Probability Distributions

Continuous Probability Distributions

Sampling Distributions

Introduction to Estimation

Introduction to Hypothesis Testing

Inference About a Population

Inference About Comparing Two Populat

Inference About Comparing Two Populat

Analysis of Variance

Simple Linear Regression and Correlat

Multiple Regression

Review of Statistical Inference

Filters

Exam 15: Chi-Squared Tests

All of the expected frequencies in a chi-squared goodness-of-fit test must be equal to each other.

To determine whether a single coin is fair, the coin was tossed 200 times. The observed frequencies with which each of the two sides of the coin turned up are recorded as 112 heads and 88 tails. Is the coin fair?

In the test of a contingency table, the expected cell frequencies must satisfy the rule of 5.

If there are only two categories, the chi-squared goodness-of-fit test is the same as the z -test for p , the population proportion (as long as the sample\cell sizes meet the conditions).

A chi-squared test statistic in a test of a contingency table that is equal to zero means:

Which of the following conditions indicate that H 0 should be rejected in a goodness-of-fit test?

A chi-squared goodness-of-fit test is always conducted as a(n):

A chi-squared test of a contingency table is applied to a contingency table with 4 rows and 4 columns for two qualitative variables. The degrees of freedom for this test must be 9.

A sports preference poll showed the following data for adults and children: Use the 5% level of significance and test to determine whether sports preferences depend on age group.

To determine the critical values in the chi-squared distribution table, you need to know the:

The expected values of a contingency table are calculated based on the assumption that H 0 is ____________________.

Explain what is meant by the rule of five and what you should do if this rule is not met.

How do you find the probabilities needed to obtain expected frequencies for a test of a contingency table?

In the test of a contingency table, the observed cell frequencies must satisfy the rule of 5.

Suppose the value of your chi-squared test statistic in a goodness-of-fit test is equal to 0. What do you conclude?

What Is Statistics

Graphical and Tabular Descriptive Techniques

Numerical Descriptive Techniques

Data Collection and Sampling

Probability

Random Variables and Discrete Probability Distributions

Continuous Probability Distributions

Sampling Distributions

Introduction to Estimation

Introduction to Hypothesis Testing

Inference About a Population

Inference About Comparing Two Populat

Inference About Comparing Two Populat

Analysis of Variance

Simple Linear Regression and Correlat

Multiple Regression

Review of Statistical Inference

Filters

Which of the following conditions indicate that H ₀ should be rejected in a goodness-of-fit test?

The expected values of a contingency table are calculated based on the assumption that H ₀ is ____________________.