Exam 17: Multiple Regression
Exam 1: What Is Statistics41 Questions
Exam 2: Graphical and Tabular Descriptive Techniques199 Questions
Exam 3: Numerical Descriptive Techniques226 Questions
Exam 4: Data Collection and Sampling82 Questions
Exam 5: Probability212 Questions
Exam 6: Random Variables and Discrete Probability Distributions174 Questions
Exam 7: Continuous Probability Distributions167 Questions
Exam 8: Sampling Distributions133 Questions
Exam 9: Introduction to Estimation88 Questions
Exam 10: Introduction to Hypothesis Testing186 Questions
Exam 11: Inference About a Population76 Questions
Exam 12: Inference About Comparing Two Populat85 Questions
Exam 13: Inference About Comparing Two Populat85 Questions
Exam 14: Analysis of Variance127 Questions
Exam 15: Chi-Squared Tests118 Questions
Exam 16: Simple Linear Regression and Correlat238 Questions
Exam 17: Multiple Regression147 Questions
Exam 18: Review of Statistical Inference189 Questions
Select questions type
Consider the following statistics of a multiple regression model: n = 25, k = 5, b 1 = - 6.31, and s e = 2.98. Can we conclude at the 1% significance level that x 1 and y are linearly related?
Free
(Essay)
4.8/5  (33)
(33)
Correct Answer:
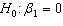 vs.
vs. 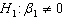 Rejection region: | t | > t 0.005,19 = 2.861 Test statistic: t = - 2.117 Conclusion: Don't reject the null hypothesis. Cannot claim a linear relationship.
Rejection region: | t | > t 0.005,19 = 2.861 Test statistic: t = - 2.117 Conclusion: Don't reject the null hypothesis. Cannot claim a linear relationship.
In a multiple regression analysis, there are 20 data points and 4 independent variables, and the sum of the squared differences between observed and predicted values of y is 180. The standard error of estimate will be:
Free
(Multiple Choice)
4.8/5  (27)
(27)
Correct Answer:
C
When an explanatory variable is dropped from a multiple regression model, the coefficient of determination can increase.
Free
(True/False)
4.7/5  (37)
(37)
Correct Answer:
False
If a group of independent variables are not significant individually but are significant as a group at a specified level of significance, this is most likely due to:
(Multiple Choice)
4.9/5  (36)
(36)
In order to test the significance of a multiple regression model involving 4 independent variables and 25 observations, the numerator and denominator degrees of freedom for the critical value of F are 3 and 21, respectively.
(True/False)
4.9/5  (35)
(35)
Student's Final Grade A statistics professor investigated some of the factors that affect an individual student's final grade in her course. She proposed the multiple regression model 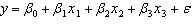 , where y is the final grade (out of 100 points), x 1 is the number of lectures skipped, x 2 is the number of late assignments, and x 3 is the midterm exam score (out of 100). The professor recorded the data for 50 randomly selected students. The computer output is shown below. THE REGRESSION EQUATION IS
, where y is the final grade (out of 100 points), x 1 is the number of lectures skipped, x 2 is the number of late assignments, and x 3 is the midterm exam score (out of 100). The professor recorded the data for 50 randomly selected students. The computer output is shown below. THE REGRESSION EQUATION IS 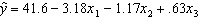
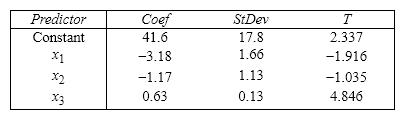 S = 13.74 R - Sq = 30.0%
ANALYSIS OF VARIANCE
S = 13.74 R - Sq = 30.0%
ANALYSIS OF VARIANCE  {Student's Final Grade Narrative} Interpret the coefficient b 2.
{Student's Final Grade Narrative} Interpret the coefficient b 2.
(Essay)
4.9/5  (25)
(25)
In a multiple regression analysis involving 4 independent variables and 30 data points, the number of degrees of freedom associated with the sum of squares for error, SSE, is 25.
(True/False)
4.9/5  (37)
(37)
A multiple regression model involves 40 observations and 4 independent variables produces a total variation in y of 100,000 and SSR = 80,400. Then, the value of MSE is 560.
(True/False)
4.8/5  (47)
(47)
In a multiple regression analysis, if the model provides a poor fit, this indicates that:
(Multiple Choice)
4.9/5  (37)
(37)
Suppose a multiple regression analysis involving 25 data points has 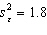 and SSE = 36. Then, the number of the independent variables must be:
and SSE = 36. Then, the number of the independent variables must be:
(Multiple Choice)
4.9/5  (30)
(30)
When the error variable does not have constant variance, this condition is called ____________________.
(Short Answer)
4.9/5  (31)
(31)
Life Expectancy An actuary wanted to develop a model to predict how long individuals will live. After consulting a number of physicians, she collected the age at death ( y ), the average number of hours of exercise per week ( x 1), the cholesterol level ( x 2), and the number of points that the individual's blood pressure exceeded the recommended value ( x 3). A random sample of 40 individuals was selected. The computer output of the multiple regression model is shown below. THE REGRESSION EQUATION IS y = 55.8 + 1.79 x 1 - 0.021 x 2 - 0.061 x 3 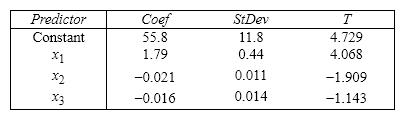 S = 9.47 R - Sq = 22.5%
ANALYSIS OF VARIANCE
S = 9.47 R - Sq = 22.5%
ANALYSIS OF VARIANCE  {Life Expectancy Narrative} Is there enough evidence at the 1% significance level to infer that the average number of hours of exercise per week and the age at death are linearly related?
{Life Expectancy Narrative} Is there enough evidence at the 1% significance level to infer that the average number of hours of exercise per week and the age at death are linearly related?
(Essay)
4.7/5  (35)
(35)
Real Estate Builder A real estate builder wishes to determine how house size is influenced by family income, family size, and education of the head of household. House size is measured in hundreds of square feet, income is measured in thousands of dollars, and education is measured in years. A partial computer output is shown below. SUMMARY OUTPUT  ANOVA
ANOVA

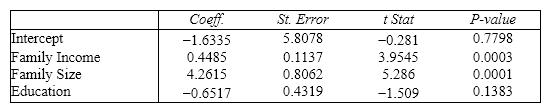 {Real Estate Builder Narrative} What minimum annual income would an individual with a family size of 4 and 16 years of education need to attain a predicted 10,000 square foot home?
{Real Estate Builder Narrative} What minimum annual income would an individual with a family size of 4 and 16 years of education need to attain a predicted 10,000 square foot home?
(Essay)
4.8/5  (39)
(39)
Marc Anthony Concert At a recent Marc Anthony concert, a survey was conducted that asked a random sample of 20 people their age and how many concerts they have attended since the first of the year. The following data were collected:  An Excel output follows:
An Excel output follows: 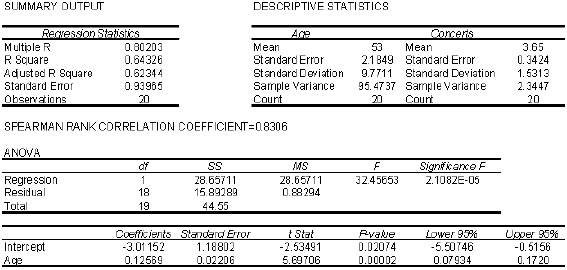 {Marc Anthony Concert Narrative} Use the residuals to compute the standardized residuals.
{Marc Anthony Concert Narrative} Use the residuals to compute the standardized residuals.
(Essay)
4.8/5  (31)
(31)
Life Expectancy An actuary wanted to develop a model to predict how long individuals will live. After consulting a number of physicians, she collected the age at death ( y ), the average number of hours of exercise per week ( x 1), the cholesterol level ( x 2), and the number of points that the individual's blood pressure exceeded the recommended value ( x 3). A random sample of 40 individuals was selected. The computer output of the multiple regression model is shown below. THE REGRESSION EQUATION IS y = 55.8 + 1.79 x 1 - 0.021 x 2 - 0.061 x 3 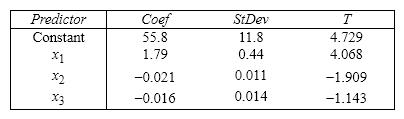 S = 9.47 R - Sq = 22.5%
ANALYSIS OF VARIANCE
S = 9.47 R - Sq = 22.5%
ANALYSIS OF VARIANCE  {Life Expectancy Narrative} Is there enough evidence at the 5% significance level to infer that the model is useful in predicting length of life?
{Life Expectancy Narrative} Is there enough evidence at the 5% significance level to infer that the model is useful in predicting length of life?
(Essay)
4.9/5  (27)
(27)
Multicollinearity is present if the dependent variable is linearly related to one of the explanatory variables.
(True/False)
4.8/5  (36)
(36)
One of the consequences of multicollinearity in multiple regression is biased estimates on the slope coefficients.
(True/False)
4.8/5  (23)
(23)
Some of the requirements for the error variable in a multiple regression model are that the standard deviation is a(n)____________________ and the errors are ____________________.
(Short Answer)
4.9/5  (47)
(47)
Showing 1 - 20 of 147
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)