Exam 11: Monte Carlo Simulation
Exam 1: Introduction30 Questions
Exam 2: Descriptive Statistics60 Questions
Exam 3: Data Visualization61 Questions
Exam 4: Linear Regression60 Questions
Exam 5: Time Series Analysis and Forecasting58 Questions
Exam 6: Data Mining60 Questions
Exam 7: Spreadsheet Models60 Questions
Exam 8: Linear Optimization Models60 Questions
Exam 9: Integer Linear Optimization Models60 Questions
Exam 10: Nonlinear Optimization Models60 Questions
Exam 11: Monte Carlo Simulation59 Questions
Exam 12: Decision Analysis60 Questions
Select questions type
Consider the table below with information regarding each activity, immediate predecessors, and duration estimates (in minutes) for each activity.
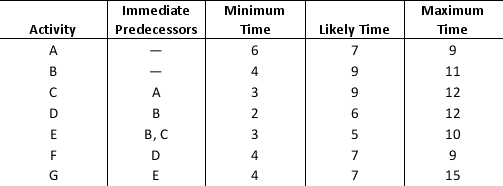
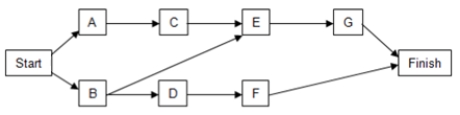 a. Using the PERT distribution in ASP to represent the duration of each activity, construct a simulation model to compute the total time to complete the task.
b. What is the expected duration of the entire project? What is the standard deviation of the project duration?
c. What is the likelihood that the project will be complete in 26 minutes?
a. Using the PERT distribution in ASP to represent the duration of each activity, construct a simulation model to compute the total time to complete the task.
b. What is the expected duration of the entire project? What is the standard deviation of the project duration?
c. What is the likelihood that the project will be complete in 26 minutes?
(Essay)
4.9/5  (39)
(39)
In a base-case scenario, the output is determined by assuming
(Multiple Choice)
4.8/5  (38)
(38)
A company has produced a new battery with an estimated mean lifetime of 60 hours. Management also believes that the standard deviation is 4.5 hours and that battery hours are normally distributed. To promote the new battery, the management has offered to refund some money if the battery fails to reach 50 hours before the battery needs to be recharged. Specifically, for batteries with a lifetime below 50 hours, the management will refund a customer $50 per hour short of 50 hours. a. For each battery sold, what is the expected cost of the promotion? b. What hours should the company set the promotion claim if it wants the expected cost to be $0.50?
(Essay)
4.8/5  (41)
(41)
A distribution of a random variable for which values extremely larger or smaller than the mean are increasingly unlikely can possibly be modeled as a(n) _____ probability distribution.
(Multiple Choice)
4.7/5  (36)
(36)
A _____ uses repeated random sampling to represent uncertainty in a model representing a real system and that computes the values of model outputs.
(Multiple Choice)
4.7/5  (50)
(50)
Which of the following inferences about a variable of interest can be drawn from the graph given below? 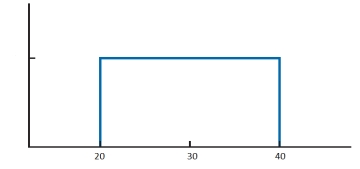
(Multiple Choice)
4.8/5  (40)
(40)
_____ is the process of determining that a simulation model provides an accurate representation of a real system.
(Multiple Choice)
4.9/5  (44)
(44)
The _____ function in Excel is used to compute the statistics required to create a histogram.
(Multiple Choice)
4.9/5  (37)
(37)
_____ is a measure of dependence between two random variables.
(Multiple Choice)
5.0/5  (29)
(29)
Reference - 11.1: Use the graph given below to answer questions 14-15.
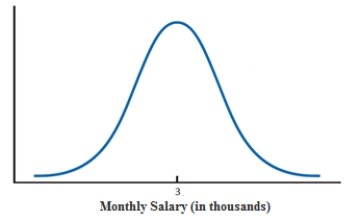 -Reference - 11.1: The type of distribution shown in the graph is
-Reference - 11.1: The type of distribution shown in the graph is
(Multiple Choice)
4.8/5  (46)
(46)
A football tournament is conducted between Team-A and Team-B of a college and the winner being the first team to win four games of seven games. The probability that Team-A wins each game are as follows:
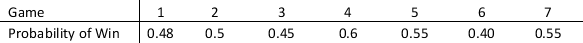 a. Set up a spreadsheet simulation model in which whether Team-A wins each game is a random variable.
b. What is the probability that the Team- A win the tournament?
c. What is the average number of games played regardless of winner?
a. Set up a spreadsheet simulation model in which whether Team-A wins each game is a random variable.
b. What is the probability that the Team- A win the tournament?
c. What is the average number of games played regardless of winner?
(Essay)
4.8/5  (36)
(36)
Reference - 11.1: Use the graph given below to answer questions 14-15.
 -Reference - 11.1: Which of the following inferences can be drawn about the monthly salary?
-Reference - 11.1: Which of the following inferences can be drawn about the monthly salary?
(Multiple Choice)
4.8/5  (26)
(26)
A distributor has generated a rough estimate of aftershave demand at their retails store. The distributor is confident that demand will range from 100 to 650. The following table lists weights for demand values within this range.
 The distributor pays a wholesale price of $21 per aftershave and then sells at a retail price of $31. a. Construct a spreadsheet model that computes net profit corresponding to a given level of demand and specified order quantity. Model demand as a random variable with ASP's custom general distribution.
b. Using simulation optimization, determine the order quantity that maximizes expected profit. What is the probability of running out of aftershave at this order quantity?
c. How many aftershaves does the distributor need to order so that the probability of running out of aftershaves is only 25 percent? How much expected profit will the distributor lose if he orders this amount rather than the amount from part b?
The distributor pays a wholesale price of $21 per aftershave and then sells at a retail price of $31. a. Construct a spreadsheet model that computes net profit corresponding to a given level of demand and specified order quantity. Model demand as a random variable with ASP's custom general distribution.
b. Using simulation optimization, determine the order quantity that maximizes expected profit. What is the probability of running out of aftershave at this order quantity?
c. How many aftershaves does the distributor need to order so that the probability of running out of aftershaves is only 25 percent? How much expected profit will the distributor lose if he orders this amount rather than the amount from part b?
(Essay)
4.9/5  (34)
(34)
Which of the following is a disadvantage of using simulation?
(Multiple Choice)
5.0/5  (40)
(40)
A company has improved its anti-virus program and has released a new version. Assume there is a 0.6 probability that the users of this anti-virus will upgrade the version in any particular year. That is, the upgrade year of the user is a geometric random variable. The revenue generated from the upgrade (when it occurs) follows a normal distribution with a mean of $80,000 and a standard deviation of $22,000.a. Complete a simulation model that analyzes the net present value of the revenue from the user upgrade. Use an annual discount rate of 8 percent.
b. What is the average net present value earned by the company?
c. What is the standard deviation of net present value?
(Essay)
4.9/5  (43)
(43)
A toy company designs a new toy car this season. The fixed cost to produce the car is $120,000. The variable cost which includes raw materials, production, and shipping costs, is $40 per car. The company will sell the car for $48 each. A distributor has agreed to pay the toy company $12 for each car remaining after the retail selling season. Forecasts are for expected sales of 55,000 toy cars with a standard deviation of 9000. The normal probability distribution is assumed to be a good description of the demand. The management has tentatively decided to produce 55,000 units (the same as average demand), but it wants to conduct an analysis regarding this production quantity before finalizing the decision.
a. Create a what-if spreadsheet model using formula that relate the values of production quantity, demand, sales, revenue from sales, amount of surplus, revenue from sales of surplus, total cost, and net profit. What is the profit corresponding to average demand (55,000 units)?
b. Modeling demand as a normal random variable with a mean of 55,000 and a standard deviation of 9000, simulate the sales of the toy car using a production quantity of 55,000 units. What is the estimate of the average profit associated with the production quantity of 55,000 cars? How does this compare to the profit corresponding to the average demand (as computed in part a)?
c. Before making a final decision on the production quantity, management wants an analysis of a more aggressive 65,000-unit production quantity and a more conservative 45,000-unit production quantity. Run your simulation with these two production quantities. What is the mean profit associated with each?
(Essay)
4.9/5  (38)
(38)
An Investment firm offers free financial planning seminars at major hotels for groups of 30 individuals. Each seminar costs them $4,000 and the average first-year commission for each new enrollment is $6,000. The firm estimates that for each individual attending the seminar, there is a 0.05 probability that he/she will enroll. a. Determine the equation for computing the profit per seminar, given values of the relevant parameters.
b. Construct a spreadsheet simulation model to analyze the profitability of the seminars. Would you recommend the investment firm to continue running the seminars?
(Essay)
4.8/5  (33)
(33)
Showing 41 - 59 of 59
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)