A fisheries biologist has been studying horseshoe crabs using categorical variables, but she has decided that reporting the data as continuous variables would be more useful. She has sampled 100 horseshoe crabs and recorded their weight (in kilograms) and width (in centimeters). The proposed regression equation is weighti = α+β × widthi + Ɛi Where the deviations Ɛi are assumed to be independent and Normally distributed with mean 0 and standard deviation σ . This model was fit to the data using the method of least squares. The following results were obtained from statistical software: \[\begin{array} { | l | c | c | } \hline \text { Variable } & \text { Estimate } & \begin{array} { c } \text { Standard Error of } \\ \text { Estimate } \end{array} \\ \hline \text { Constant } & 2.3013 & 0.9788 \\ \text { Width } & 0.7963 & 0.0939 \\ \hline \end{array}\] r2 = 0.423, s = 2.2018. Suppose we use statistical software to predict the weight for a horseshoe crab with width 2.25 centimeters, which yields the following: \[\begin{array} { | c | c | c | c | } \hline \text { Predicted Weight } & \begin{array} { c } \text { Std Error } \\ \text { Predict } \end{array} & \mathbf { 9 5 . 0 \% } \text { CI } & \mathbf { 9 5 . 0 \% } \text { PI } \\ \hline 4.093 & 0.774 & ( 2.556,5.630 ) & ( - 0.539,8.725 ) \\ \hline \end{array}\] What is a 95% interval for this prediction according to this output?

A) (2.556, 5.630) B) (-0.539, 8.725) C) 4.093 ± 1.9419 D) 4.093 ± 0.1863 A) (2.556, 5.630) B) (-0.539, 8.725) C) 4.093 ± 1.9419 D) 4.093 ± 0.1863

A researcher from the crop and soil sciences department at your local university is interested in the relationship between the amount of phosphorus and nitrogen found in the ground. She takes a random sample of sites in the Commonwealth of Virginia and fits a linear regression model to the data. Based on this model, she obtains the following prediction results: \[\begin{array} { | c | c | c | c | c | } \hline \text { Nitrogen Level } & \begin{array} { c } \text { Predicted } \\ \text { Phosphorus Level } \end{array} & \begin{array} { c } \text { Std Error } \\ \text { Predict } \end{array} & \mathbf { 9 5 . 0 \% } \text { CI } & \mathbf { 9 5 . 0 \% } \text { PI } \\ \hline 20 & 15 & 1.25 & ( 12,18 ) & ( 10,20 ) \\ \hline \end{array}\] Suppose we wish to predict the phosphorus level of a particular site that had a nitrogen level of 20. What is a 95% interval for the prediction for this site?

A) (12, 18) B) (10, 20) C) 15 ± 1.25 D) 15 ± 2.49 A) (12, 18) B) (10, 20) C) 15 ± 1.25 D) 15 ± 2.49

Exam 21: Inference for Regression

Data on the water quality in the eastern United States were obtained by a researcher who wanted to ascertain whether the amount of particulates in water (ppm) could be used to accurately predict the water quality score. Suppose we use the following simple linear regression model: Quality_i = α+ β× particulates_i + Ɛ_i Where the deviations Ɛ_i are assumed to be independent and Normally distributed with mean 0 and standard deviation σ. This model was fit to the data using the method of least squares. The following results were obtained from statistical software based on a sample of size 61: Variable Estimate Standard Error of Estimate Constant 6.214 1.003 Particulates -0.009 0.020 r² = 0.005, s = 0.7896. Suppose the researcher tests the following hypotheses: H₀: β₁ = 0, H_a: β₁ 0 What is the value of the t statistic for this test?

(Multiple Choice)

4.8/5

(30)

Question 21

Researchers examined hormonal changes in 39 women during the menopausal years. They found a weak linear relationship between age (in years) and the six-month percent change in plasma level of the reproductive hormone LH (luteinizing hormone). Software gives the following output for a least-squares regression analysis: Predictor Coef SE Coef T P Constant 101.46 79.05 1.28 0.207 age -1.627 1.559 -1.04 0.303 S = 41.5236 R-Sq = 2.9% R-Sq(adj) = 0.2% Based on this output, when testing the hypotheses H₀: β₁ = 0 versus H_a: β₁ ≠ 0, the value of the t statistic is ______________.

(Short Answer)

4.8/5

(37)

Question 22

A fisheries biologist has been studying horseshoe crabs using categorical variables, but she has decided that reporting the data as continuous variables would be more useful. She has sampled 100 horseshoe crabs and recorded their weight (in kilograms) and width (in centimeters). The proposed regression equation is weight_i = α+β × width_i + Ɛ_i Where the deviations Ɛ_i are assumed to be independent and Normally distributed with mean 0 and standard deviation σ . This model was fit to the data using the method of least squares. The following results were obtained from statistical software: Variable Estimate Standard Error of Estimate Constant 2.3013 0.9788 Width 0.7963 0.0939 r² = 0.423, s = 2.2018. Suppose we use statistical software to predict the weight for a horseshoe crab with width 2.25 centimeters, which yields the following: Predicted Weight Std Error Predict CI PI 4.093 0.774 (2.556,5.630) (-0.539,8.725) What is a 95% interval for this prediction according to this output?

(Multiple Choice)

4.8/5

(28)

Question 23

Researchers examined hormonal changes in 39 women during the menopausal years. They found a weak linear relationship between age (in years) and the six-month percent change in plasma level of the reproductive hormone LH (luteinizing hormone). Software gives the following output for a least-squares regression analysis: Predictor Coef SE Coef Constant 101.46 79.05 1.28 0.207 age -1.627 1.559 -1.04 0.303 S = 41.5236 R-Sq = 2.9% R-Sq(adj) = 0.2% Using a significance level of 0.05, which of the following conclusions best describes the findings?

(Multiple Choice)

4.9/5

(25)

Question 24

A random sample of 79 patients from a walk-in clinic records the low- and high-density cholesterol levels of the patients, labeled LDL and HDL, respectively. LDL is often referred to as "bad" cholesterol, while HDL is often referred to as "good" cholesterol. A researcher is interested in fitting the following linear regression curve to LDL and HDL levels: LDL_i = α+ β× HDL_i + Ɛ_i Where the deviations Ɛ_i are assumed to be independent and Normally distributed with mean 0 and standard deviation σ. This model was fit to the data using the method of least squares. The following results were obtained from statistical software: Variable Estimate Standard Error of Estimate Constant -25 3.000 HDL 0.75 0.025 r² = 0.810, s = 50. What is a 90% confidence interval for the slope β₁ in the simple linear regression model?

(Multiple Choice)

4.8/5

(28)

Question 25

Researchers examined hormonal changes in 39 women during the menopausal years. They found a weak linear relationship between age (in years) and the six-month percent change in plasma level of the reproductive hormone LH (luteinizing hormone). Software gives the following output for a least-squares regression analysis: Predictor Coef SE Coef T P Constant 101.46 79.05 1.28 0.207 Age -1.627 1.559 -1.04 0.303 S = 41.5236 R-Sq = 2.9% R-Sq(adj) = 0.2% What is the margin of error for a 95% confidence interval for the slope βin the linear regression model?

(Multiple Choice)

4.8/5

(26)

Question 26

A fisheries biologist has been studying horseshoe crabs using categorical variables, but she has decided that reporting the data as continuous variables would be more useful. She has sampled 100 horseshoe crabs and recorded their weight (in kilograms) and width (in centimeters). The proposed regression equation is Weight_i = α+β × width_i + Ɛ_i Where the deviations Ɛ_i are assumed to be independent and Normally distributed with mean 0 and standard deviation σ. This model was fit to the data using the method of least squares. The following results were obtained from statistical software: Variable Estimate Standard Error of Estimate Constant 2.3013 0.9788 Width 0.7963 0.0939 r² = 0.423, s = 2.2018. The quantity s = 2.2018 is an estimate of the standard deviation, , of the deviations in the simple linear regression model. What is the degrees of freedom for s?

(Multiple Choice)

4.9/5

(38)

Question 27

To estimate an individual response, we use a confidence interval.

(True/False)

4.7/5

(40)

Question 28

Tail-feather length in birds is sometimes a sexually dimorphic trait; that is, the trait differs substantially for males and for females of the same species. Researchers studied the relationship between tail-feather length (measuring the R1 central tail feather) and weight in a sample of 20 male long-tailed finches raised in an aviary. The data are displayed in the scatterplot below, followed with software output about the least-squares regression model of feather length as a function of weight. $Tail-feather length in birds is sometimes a sexually dimorphic trait; that is, the trait differs substantially for males and for females of the same species. Researchers studied the relationship between tail-feather length (measuring the R1 central tail feather) and weight in a sample of 20 male long-tailed finches raised in an aviary. The data are displayed in the scatterplot below, followed with software output about the least-squares regression model of feather length as a function of weight. 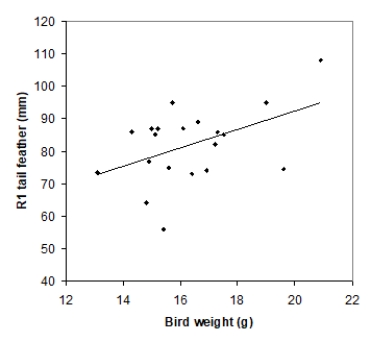\begin{array}{l} \begin{array} { l l r } \hline &\text {Coefficients }&\text {Standard Error }\\ \hline\text {Intercept }&35.7379 & 21.0523 \\ \text { Bird-weight}&2.8299 & 1.2811\\ \hline\text {R Square }&0.2133\\ \text {Standard Error }&\ 10.5270\ \end{array} \end{array} What percentage of variation in tail-feather length that can be explained by this linear model?$ Coefficients Standard Error Intercept 35.7379 21.0523 Bird-weight 2.8299 1.2811 R Square 0.2133 Standard Error \ 10.5270\ What percentage of variation in tail-feather length that can be explained by this linear model?

(Multiple Choice)

5.0/5

(31)

Question 29

Data on the water quality in the eastern United States were obtained by a researcher who wanted to ascertain whether the amount of particulates in water (ppm) could be used to accurately predict the water quality score. Suppose we use the following simple linear regression model: Quality_i = α+ β× particulates_i + Ɛ_i Where the deviations Ɛ_i are assumed to be independent and Normally distributed with mean 0 and standard deviation σ. This model was fit to the data using the method of least squares. The following results were obtained from statistical software based on a sample of size 61: Variable Estimate Standard Error of Estimate Constant 6.214 1.003 Particulates -0.009 0.020 r² = 0.005, s = 0.7896. What is a 90% confidence interval for the slope in the simple linear regression model?

(Multiple Choice)

4.7/5

(39)

Question 30

A researcher from the crop and soil sciences department at your local university is interested in the relationship between the amount of phosphorus and nitrogen found in the ground. She takes a random sample of sites in the Commonwealth of Virginia and fits a linear regression model to the data. Based on this model, she obtains the following prediction results: Nitrogen Level Predicted Phosphorus Level Std Error Predict CI PI 20 15 1.25 (12,18) (10,20) Suppose we wish to predict the phosphorus level of a particular site that had a nitrogen level of 20. What is a 95% interval for the prediction for this site?

(Multiple Choice)

4.9/5

(32)

Question 31

Tail-feather length in birds is sometimes a sexually dimorphic trait; that is, the trait differs substantially for males and for females. Researchers studied the relationship between weight (x) and tail-feather length (y) in a sample of 5 wild male long-tailed finches. Here are the data: weight () tail length () 20.8 82.5 19.1 82.5 15.9 67.0 16.7 70.5 15.7 73.5 Using appropriate software, what is the numerical value of the y intercept for the least-squares regression line?

(Multiple Choice)

4.9/5

(39)

Question 32

Before surgical removal of a diseased parathyroid gland, two tests are often performed: the standard intact test and the turbo test. Both tests measure parathyroid hormone (PTH, in ng/L), but the turbo test is very expensive. Researchers obtained data from both tests in a sample of 48 patients to predict turbo test results (y) from standard intact test results (x). The published findings include a scatterplot showing a clear linear relationship and the following summary: Y = 1.08x - 4.36 (r = 0.97; n = 48) We want to test a hypothesis of no relationship between the two procedures, H₀: p= 0 versus H_a: p≠0. What is the P-value for this test?

(Multiple Choice)

4.9/5

(40)

Question 33

Data on the water quality in the eastern United States were obtained by a researcher who wanted to ascertain whether the amount of particulates in water (ppm) could be used to accurately predict the water quality score. Suppose we use the following simple linear regression model: Quality_i = α+ β× particulates_i + Ɛ_i Where the deviations Ɛ_i are assumed to be independent and Normally distributed with mean 0 and standard deviation σ. This model was fit to the data using the method of least squares. The following results were obtained from statistical software based on a sample of size 61: Variable Estimate Standard Error of Estimate Constant 6.214 1.003 Particulates -0.009 0.020 r² = 0.005, s = 0.7896. Here is a scatterplot of the amount of particulates versus water quality: $Data on the water quality in the eastern United States were obtained by a researcher who wanted to ascertain whether the amount of particulates in water (ppm) could be used to accurately predict the water quality score. Suppose we use the following simple linear regression model: Qualityi = α+ β× particulatesi + Ɛi Where the deviations Ɛi are assumed to be independent and Normally distributed with mean 0 and standard deviation σ. This model was fit to the data using the method of least squares. The following results were obtained from statistical software based on a sample of size 61: \begin{array} { | l | c | c | } \hline \text { Variable } & \text { Estimate } & \begin{array} { c } \text { Standard Error of } \\ \text { Estimate } \end{array} \\ \hline \text { Constant } & 6.214 & 1.003 \\ \text { Particulates } & - 0.009 & 0.020 \\ \hline \end{array} r2 = 0.005, s = 0.7896. Here is a scatterplot of the amount of particulates versus water quality: 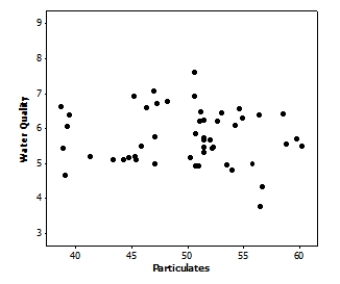Which of the following statements is supported by the plot?$ Which of the following statements is supported by the plot?

(Multiple Choice)

4.9/5

(31)

Question 34

Tail-feather length in birds is sometimes a sexually dimorphic trait; that is, the trait differs substantially for males and for females of the same species. Researchers studied the relationship between tail-feather length (measuring the R1 central tail feather) and weight in a sample of 20 male long-tailed finches raised in an aviary. The data are displayed in the scatterplot below, followed with software output about the least-squares regression model of feather length as a function of weight. $Tail-feather length in birds is sometimes a sexually dimorphic trait; that is, the trait differs substantially for males and for females of the same species. Researchers studied the relationship between tail-feather length (measuring the R1 central tail feather) and weight in a sample of 20 male long-tailed finches raised in an aviary. The data are displayed in the scatterplot below, followed with software output about the least-squares regression model of feather length as a function of weight. 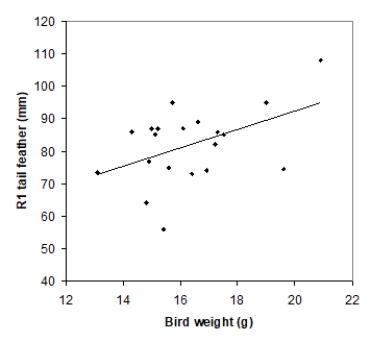\begin{array}{l} \begin{array} { l l r } \hline &\text {Coefficients }&\text {Standard Error }\\ \hline\text {Intercept }&35.7379 & 21.0523 \\ \text { Bird-weight}&2.8299 & 1.2811\\ \hline\text {R Square }&0.2133\\ \text {Standard Error }&\ 10.5270\ \end{array} \end{array} What is the margin of error for a 95% confidence interval for the true population slope β in this linear regression model?$ Coefficients Standard Error Intercept 35.7379 21.0523 Bird-weight 2.8299 1.2811 R Square 0.2133 Standard Error \ 10.5270\ What is the margin of error for a 95% confidence interval for the true population slope β in this linear regression model?

(Multiple Choice)

4.8/5

(36)

Question 35

The slope βof the population regression line is exactly 0 when the correlation = 0

(True/False)

4.8/5

(42)

Question 36

Researchers examined hormonal changes in 39 women during the menopausal years. They found a weak linear relationship between age (in years) and the six-month percent change in plasma level of the reproductive hormone LH (luteinizing hormone). Software gives the following output for a least-squares regression analysis: Predictor Coef SE Coef Constant 101.46 79.05 1.28 0.207 age -1.627 1.559 -1.04 0.303 S = 41.5236 R-Sq = 2.9% R-Sq(adj) = 0.2% Based on this output, the slope of the least-squares regression line is ______________.

(Short Answer)

4.8/5

(33)

Question 37

Tail-feather length in birds is sometimes a sexually dimorphic trait; that is, the trait differs substantially for males and for females of the same species. Researchers studied the relationship between tail-feather length (measuring the R1 central tail feather) and weight in a sample of 20 male long-tailed finches raised in an aviary. The data are displayed in the scatterplot below, followed with software output about the least-squares regression model of feather length as a function of weight. $Tail-feather length in birds is sometimes a sexually dimorphic trait; that is, the trait differs substantially for males and for females of the same species. Researchers studied the relationship between tail-feather length (measuring the R1 central tail feather) and weight in a sample of 20 male long-tailed finches raised in an aviary. The data are displayed in the scatterplot below, followed with software output about the least-squares regression model of feather length as a function of weight. 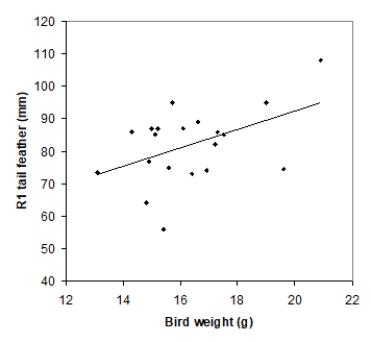\begin{array}{l} \begin{array} { l l r } \hline &\text {Coefficients }&\text {Standard Error }\\ \hline\text {Intercept }&35.7379 & 21.0523 \\ \text { Bird-weight}&2.8299 & 1.2811\\ \hline\text {R Square }&0.2133\\ \text {Standard Error }&\ 10.5270\ \end{array} \end{array} What does the standard error value of 10.5270 represent?$ Coefficients Standard Error Intercept 35.7379 21.0523 Bird-weight 2.8299 1.2811 R Square 0.2133 Standard Error \ 10.5270\ What does the standard error value of 10.5270 represent?

(Multiple Choice)

4.7/5

(24)

Question 38

A fisheries biologist has been studying horseshoe crabs using categorical variables, but she has decided that reporting the data as continuous variables would be more useful. She has sampled 100 horseshoe crabs and recorded their weight (in kilograms) and width (in centimeters). The proposed regression equation is Weight_i = α+β × width_i + Ɛ_i Where the deviations Ɛ_i are assumed to be independent and Normally distributed with mean 0 and standard deviation σ. This model was fit to the data using the method of least squares. The following results were obtained from statistical software: Variable Estimate Standard Error of Estimate Constant 2.3013 0.9788 Width 0.7963 0.0939 r² = 0.423, s = 2.2018. What is intercept of the least-squares regression line?

(Multiple Choice)

4.8/5

(38)

Question 39

Researchers want to know if reading skills can explain IQ test scores in children with dyslexia. The following scatterplot examines the relationship between reading skill score and IQ test score for 22 dyslexic children. The least-squares regression line is displayed on the plot, along with the value of r². $Researchers want to know if reading skills can explain IQ test scores in children with dyslexia. The following scatterplot examines the relationship between reading skill score and IQ test score for 22 dyslexic children. The least-squares regression line is displayed on the plot, along with the value of r2. 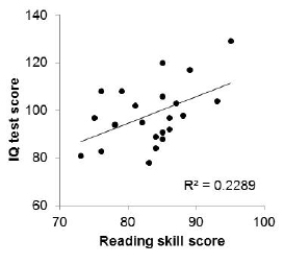Here is software output for predicting IQ test score when reading skill score = 80: \begin{array} { l l l l l } \text { Obs } & \text { Fit } & \text { SE Fit } & 95 \% \text { CI } & 95 \% \text { PI } \\ 80.0 & 94.59 & 2.94 & ( 88.46,100.71 ) & ( 69.44,119.74 ) \end{array} What is the best description of the interval (69.44, 119.74)?$ Here is software output for predicting IQ test score when reading skill score = 80: Obs Fit SE Fit 95\% CI 95\% PI 80.0 94.59 2.94 (88.46,100.71) (69.44,119.74) What is the best description of the interval (69.44, 119.74)?

(Multiple Choice)

4.8/5

(41)

Question 40

Showing 21 - 40 of 45

To estimate an individual response, we use a confidence interval.

The slope βof the population regression line is exactly 0 when the correlation = 0

Picturing Distributions With Graphs

Describing Quantitative Distributions With Numbers

Scatterplots and Correlation

Regression

Two-Way Tables

Samples and Observational Studies

Designing Experiments

Essential Probability Rules

Independence and Conditional Probabilities

The Normal Distributions

Discrete Probability Distributions

Sampling Distributions

Introduction to Inference

Exercises

Inference About a Population Mean

Comparing Two Means

Inference About a Population Proportion

Comparing Two Proportions

The Chi-Square Test for Goodness of Fit

The Chi-Square Test for Two-Way Tables

One-Way Analysis of Variance: Comparing Several Means

More About Analysis of Variance: Follow-Up Tests and Two-Way Anova

Nonparametric Tests

Multiple and Logistic Regression

Filters