Exam 5: Linear Inequalities and Linear Programming
Exam 1: Linear Equations and Graphs59 Questions
Exam 2: Functions and Graphs178 Questions
Exam 3: Mathematics of Finance57 Questions
Exam 4: Systems of Linear Equations; Matrices115 Questions
Exam 5: Linear Inequalities and Linear Programming26 Questions
Exam 6: Linear Programming: The Simplex Method58 Questions
Exam 7: Logic, Sets, and Counting51 Questions
Exam 8: Probability59 Questions
Exam 9: Markov Chains60 Questions
Exam 10: Data Description and Probability Distributions65 Questions
Exam 11: Games and Decisions52 Questions
Exam 12: Appendix A: Basic Algebra Review45 Questions
Exam 13: Appendix B: Special Topics20 Questions
Select questions type
Formulate the following problem as a linear programming problem (DO NOT SOLVE).A company which produces three kinds of spaghetti sauce has two plants. The East plant produces 3,500 jars of plain sauce, 6,500 jars of sauce with mushrooms, and 3,000 jars of hot spicy sauce per day. The West plant produces 2,500 jars of plain sauce, 2,000 jars of sauce with mushrooms, and 1,500 jars of hot spicy sauce per day. The cost to operate the East plant is $8,500 per day and the cost to operate the West plant is $9,500 per day. How many days should each plant operate to minimize cost and to fill an order for at least 8,000 jars of plain sauce, 9,000 jars of sauce with mushrooms, and 6,000 jars of hot spicy sauce? (Let 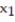 equal the number of days East plant should operate and
equal the number of days East plant should operate and 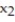 the number of days West plant should operate.)
the number of days West plant should operate.)
(Short Answer)
4.9/5  (26)
(26)
Use graphical methods to solve the linear programming problem:
-A math camp wants to hire counselors and aides to fill its staffing needs at minimum cost. The average monthly salary of a counselor is $2400 and the average monthly salary of an aide is $1100. The camp can accommodate up to 45 staff members and needs at least 30 to run properly. They must have at least 10 aides, and may have up to 3 aides for every 2 counselors. How many counselors and how many aides should the camp hire to minimize cost?
(Multiple Choice)
4.9/5  (41)
(41)
Graph the solution set of the system of linear inequalities and indicate whether the solution region is bounded or unbounded:
-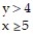
(Multiple Choice)
4.9/5  (33)
(33)
Formulate the following problem as a linear programming problem (DO NOT SOLVE):A steel company produces two types of machine dies, part A and part B. Part A requires 6 hours of casting time and 4 hours of firing time. Part B requires 8 hours of casting time and 3 hours of firing time. The maximum number of hours per week available for casting and firing are 85 and 70, respectively. The company makes a $2.00 profit on each part A that it produces, and a $6.00 profit on each part B that it produces. How many of each type should the company produce each week in order to maximize its profit? (Let 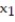 equal the number of A parts and
equal the number of A parts and 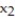 equal the number of B parts produced each week.)
equal the number of B parts produced each week.)
(Short Answer)
4.8/5  (41)
(41)
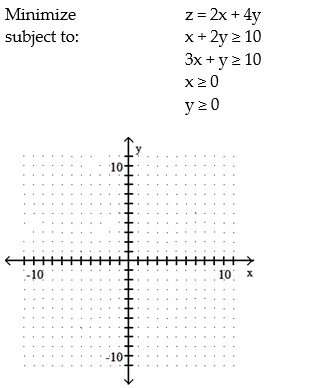
Use graphical methods to solve the linear programming problem:
-
(Multiple Choice)
4.8/5  (37)
(37)
Graph the solution set of the system of linear inequalities and indicate whether the solution region is bounded or unbounded:
-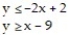
(Multiple Choice)
4.8/5  (29)
(29)
Showing 21 - 26 of 26
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)