Exam 12: Modeling Randomness

John is taking Statistics and Biology this semester. The probability John will get an A in Statistics is 0.4. The probability John will get an A in Biology is 0.3. The probability John will get an A in both Statistics and Biology is 0.15. What is the probability that John will get at least one A between his Statistics and Biology courses?

Let X be the amount in claims (in dollars) that a randomly chosen policyholder collects from an insurance company this year. The probability distribution function of X is given below. -Let $S be the standard deviation of X. Which of the following is a correct interpretation of this value?

A tire manufacturer designed a new tread pattern for its all-weather tires. Repeated tests were conducted on cars of approximately the same weight traveling at 60 miles per hour. The tests showed that the new tread pattern enables the cars to stop completely in an average distance of 125 feet with a standard deviation of 6.5 feet and that the stopping distances are approximately normally distributed. -One car tested had a stopping distance of 112 feet. How many standard deviations was this car away from the mean stopping distance?

A soft drink company holds a contest in which a prize may be revealed on the inside of the bottle cap. The probability that each bottle cap reveals a prize is 0.39, and winning is independent from one bottle to the next. You buy six bottles. Let X be the number of prizes you win. -What is the distribution of X?

An online psychic (psi) ability or extrasensory perception (ESP) test shows the participant five face-down cards on the screen and asks the participant to "click on the one card that has a picture on the other side." After clicking a card, the test shows you the card to determine if your guess was correct. -If a person does not have ESP, what is the probability the person's guess is correct?

Based on her past experience, a professor knows that the probability distribution function for X = number of students who come to her office hours on any given Wednesday is given below. -The standard deviation of X is 0.96. Interpret this value in the context of the problem.

A soft drink company holds a contest in which a prize may be revealed on the inside of the bottle cap. The probability that each bottle cap reveals a prize is 0.39, and winning is independent from one bottle to the next. You buy six bottles. Let X be the number of prizes you win. -Identify the parameter values for the distribution of X. n = π =

Suppose that only 8% of a large population has a certain disease. A diagnostic test has been developed which is 90% accurate for people with the disease (90% of people with the disease test positive), and 85% accurate for people without the disease (85% of people without the disease test negative). Define the following events: A = person has the disease B = person tests positive on the diagnostic test -For each of the given probabilities, state whether the probability is a conditional probability or an unconditional probability: 0.08? 0.90? 0.85?

The volume in a can of soda is normally distributed with mean 358 mililiters (ml) and standard deviation 6 ml. -Use the Normal Probability Calculator applet to calculate the probability that a randomly chosen can of soda is filled with less than 350 ml of soda.

Suppose that 45% of customers at the local farmer's market prefer plastic bags to paper bags, whereas 62% of customers at the local grocery store prefer plastic bags to paper bags. You plan to take a simple random sample of 40 farmer's market customers and 40 grocery story customers and survey their bag preferences. Define p ̂_F-p ̂_G as the difference in sample proportions that prefer plastic bags to paper bags between the two locations (farmer's market - grocery store). -Calculate μ_(p_F-p_G ).

There are ten Academic Senate faculty in the Statistics Department at the University of California, Irvine: three females and seven males. Two faculty are to be selected without replacement to serve on a committee where one of those selected will serve as the head of the committee. -A simulation of this random process was run 1,000 times, and the number of females selected for the committee was recorded on each simulation. A bar plot of the results follows. 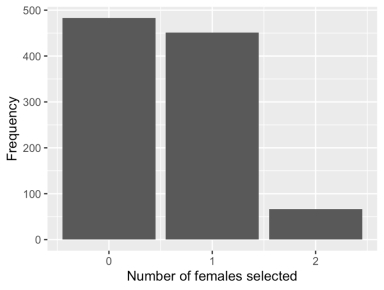Use the bar plot to estimate the probability that zero females are selected for the committee.

Math SAT scores for students admitted to University A are bell-shaped with a mean of 520 and a standard deviation of 60. Math SAT scores for students admitted to University B are also bell-shaped, but with a mean of 580 and a standard deviation of 45. Suppose you plan to take a simple random sample of 15 students from University A and 25 students from University B. Let x_B-x_A be the difference in sample mean math SAT scores between the two samples (B - A). -If you were to take a very large number of samples, about how far away would you expect x_B-x_A to fall from its mean?

A soft drink company holds a contest in which a prize may be revealed on the inside of the bottle cap. The probability that each bottle cap reveals a prize is 0.39, and winning is independent from one bottle to the next. You buy six bottles. Let X be the number of prizes you win. -Again buy six bottles, but now define the random variable Y = the number of bottles with no prize. Identify the parameter values for the distribution of X. n = ? =

Let X be the amount in claims (in dollars) that a randomly chosen policyholder collects from an insurance company this year. The probability distribution function of X is given below. -Calculate the standard deviation of X. $________

An "instant lottery" is played by buying a ticket and scratching off a coating to reveal whether or not you have won a prize, and if so, how much. Suppose an instant lottery pays $5 with probability 0.05 and $100 with probability 0.006. Otherwise it pays nothing. Define X = amount won for a single ticket. (You can ignore the cost of the ticket.) -Fill in the blank with the correct dollar amount: If the lottery agency does not want to lose money over the long run, they must charge at least $_______ per ticket.

Suppose that only 8% of a large population has a certain disease. A diagnostic test has been developed which is 90% accurate for people with the disease (90% of people with the disease test positive), and 85% accurate for people without the disease (85% of people without the disease test negative). Define the following events: A = person has the disease B = person tests positive on the diagnostic test -Given that a person tests positive on the diagnostic test, what is the probability he or she has the disease?

Let X = the average number of miles per day put on a typical one of the company's rental car in a year (365 days). What is the standard deviation of X?

In a large population of college students, 56% live in a campus residence hall, 62% participate in a campus meal program, and 42% do both. Define events R = student lives in a campus residence hall M = student participates in a campus meal program -Find P(R│M)..

Assume that, for events and , and . Are and are mutually exclusive?

Suppose you roll a six-sided die once. Define events A = roll an even number B = roll a two C = roll an odd number D = roll a number greater than three -Are events B and C mutually exclusive?